バイラテラルフィルタをPythonで、OpenCVを使わず記述してみます。
以前の記事でPythonでの記述をしてみましたが、効果確認程度に動く程度のものだったので、もう少し真面目に記述してみようと思います。
アルゴリズム
詳細は割愛します。以前の記事を書いた際に、その中身はなんとなくわかった気になっているので、ここではアルゴリズムの説明ではなくPythonコードの記述に専念します。
コード
すこし真面目に書きました。大きな間違いはないと思うんだけどなぁ。
import cv2
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import itertools
###########################################################
# ガウシアンフィルタを作成する関数
# size : kernelのサイズの半分(size*2+1)の大きさのフィルタを返す
# sigma : ガウス分布の偏差
# show : グラフ表示フラグ(1で表示 for debug)
###########################################################
def create_gausfilter(size,sigma,show=0):
X,Y = np.meshgrid(np.arange(-size,size+1),np.arange(-size,size+1))
Z = np.sqrt(X**2+Y**2) #中心からの距離情報へ変換
gaus = np.exp(-(Z/size)**2 / (size*sigma**2))
#3次元グラフ表示(for debug)
if show == 1:
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(X, Y, gaus)
# ax.contourf(X, Y, gaus, zdir='gaus', offset=0, cmap=plt.cm.hot)
# ax.set_zlim(0, 1)
plt.show()
return gaus
###########################################################
# ガウシアンの結果をLUTに保存(255indexで値も255に正規化)
# sigma : ガウス分布の偏差
# show : グラフ表示フラグ(1で表示 for debug)
###########################################################
def create_gauslut(sigma,show=0):
lut = np.arange(0,256,1)
lut = (255*np.exp(-(lut/255)**2 / (2*sigma**2)))
#グラフ表示(for debug)
if show == 1:
plt.figure()
plt.plot(lut)
return lut
###########################################################
# バイラテラルフィルタ
# img : 入力画像
# size : フィルタサイズの半径(カーネルサイズは2*size+1)
# sigmaColor : 色空間におけるフィルタシグマ.このパラメータが大きくなると,ピクセル近傍内にある,色的により遠くのピクセルが混ぜ合わせられ,結果として同じような色の領域がより大きくなります.
# sigmaSpace : 座標空間におけるフィルタシグマ.このパラメータが大きくなると,より遠くのピクセル同士が影響を及ぼしあいます.
# show : グラフ表示フラグ(1で表示 for debug)
###########################################################
def bilateralfilter(img, size, sigmaColor, sigmaSpace,show=0):
kernel_size = size*2+1 #フィルタのカーネルサイズ
img = img.astype(np.int32) #符号付きdiffを取るのでsinged 32bit
lut = create_gauslut(sigmaColor,show)
gaus = create_gausfilter(size,sigmaSpace,show)
#バイラテラル的には外の値の違う画素は仲間に入らないので、255にする必要はないかもしれない
img_big = np.full((img.shape[0]+kernel_size,img.shape[1]+kernel_size,img.shape[2]),255,dtype=np.int32) #周りを白埋め
img_big[size:-size-1,size:-size-1,:] = img #中心に画像をはめ込む
sums = np.zeros_like(img) #合計値保存用
divs = np.zeros_like(img) #剰数保存用
for x, y in itertools.product(range(kernel_size), range(kernel_size)):
dif = lut[abs(img - img_big[y:y-kernel_size,x:x-kernel_size,:])]
gau = (gaus[x][y]*dif).astype(np.int32)
sums += gau*img_big[y:y-kernel_size,x:x-kernel_size,:]
divs += gau
return (sums/divs).astype(np.uint8)
if __name__ == '__main__':
img = cv2.imread("IMG_0001.jpg")
out = bilateralfilter(img,5,0.4,0.4,1)
cv2.imwrite("out.jpg",out)
説明
create_gausfilter()
ガウシアンフィルタをパラメータに応じて動的に作るようにしました。フィルタのサイズと標準偏差を指定すると、それに基づいて正規分布を作り、その形をフィルタにします。このフィルタは浮動小数点としました。
指定するサイズはフィルタの半径、すなわち指定したサイズの倍(厳密には倍+1)の大きさのフィルタが作られます。例えば5を指定すると、11×11のフィルタが作られます。中心からの距離で作りたかったので、奇数縛りを入れるためです。
まず、フィルタの中心からの距離を求めます。そのために、まずmeshgridを使って、中心からのx方向、y方向の距離が記述された配列を作ります。
X,Y = np.meshgrid(np.arange(-3,4),np.arange(-3,4))
と指定してやると、Xとして
[[-3 -2 -1 0 1 2 3]
[-3 -2 -1 0 1 2 3]
[-3 -2 -1 0 1 2 3]
[-3 -2 -1 0 1 2 3]
[-3 -2 -1 0 1 2 3]
[-3 -2 -1 0 1 2 3]
[-3 -2 -1 0 1 2 3]]こんな感じ、Yとして
[[-3 -3 -3 -3 -3 -3 -3]
[-2 -2 -2 -2 -2 -2 -2]
[-1 -1 -1 -1 -1 -1 -1]
[ 0 0 0 0 0 0 0]
[ 1 1 1 1 1 1 1]
[ 2 2 2 2 2 2 2]
[ 3 3 3 3 3 3 3]]こんな感じの配列が作られます。面白いですね。meshgridってこんな用途で使うんでしょうね。この配列が意味するのは中心からの、x,yそれぞれの距離になります。この2つの配列から、
Z = np.sqrt(X ** 2 + Y ** 2)
この計算で中心からの距離が求まります。
[[4.242 3.605 3.162 3. 3.162 3.605 4.242]
[3.605 2.828 2.236 2. 2.236 2.828 3.605]
[3.162 2.236 1.414 1. 1.414 2.236 3.162]
[3. 2. 1. 0. 1. 2. 3. ]
[3.162 2.236 1.414 1. 1.414 2.236 3.162]
[3.605 2.828 2.236 2. 2.236 2.828 3.605]
[4.242 3.605 3.162 3. 3.162 3.605 4.242]]こんな感じ。この距離を元に、適当な標準偏差(0.3)でガウス関数をかけるとこんな感じのグラフが書けます。ここではいったん、フィルタの半径を1に正規化したうえで、標準偏差を指定することにしました。
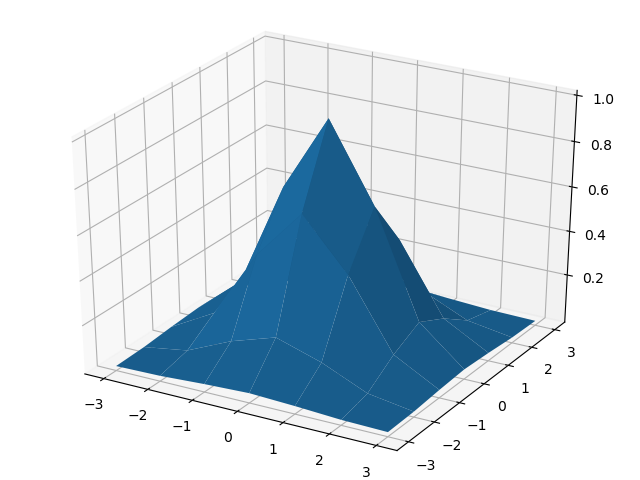
サイズが小さいので少しいびつですが、もう少しでかいサイズにすると、こんな感じになり、まぁあってそうな気がします。
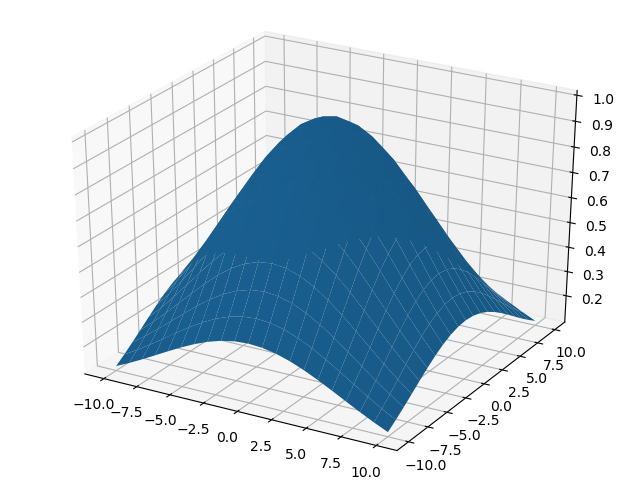
この3次元グラフですが、ちょっと使い方がわかっておらず、どこぞのソースのコピペ気味ですが、
from mpl_toolkits.mplot3d import Axes3D
をimportしてあげると、
ax = Axes3D(fig)
な関数が使えて、こいつに対して、
ax.plot_surface(X, Y, gaus)
と3次元分のデータを渡してあげると、描画してくれるようです。グラフに対して、装飾もいろいろできるようですが、今回深追いはしません。シンプルに終わらせます。
create_gauslut()
今度は、色の差に応じた重みを付けるためのガウスの方です。基本的には先の記事で書いた記述と同じです。
こちらは1次元なので、比較的シンプルに、差分0から255までの距離に応じて、正規分布を作ります。差の絶対値を使うことにしたので、正の方向だけにしています。floatの配列にしました。
ここでガウス関数のテーブルを事前に作っておく理由は、全画素毎にまじめにnp.exp()を呼んでたらどえらい処理時間がかかるので、先に計算結果を入れておくルックアップテーブルを用意しておき、それを引く形で時間節約するためです。
横軸は1を255に正規化しています。sigma = 0.3で描画してみると、こんな感じ。まぁこんなもんかな。
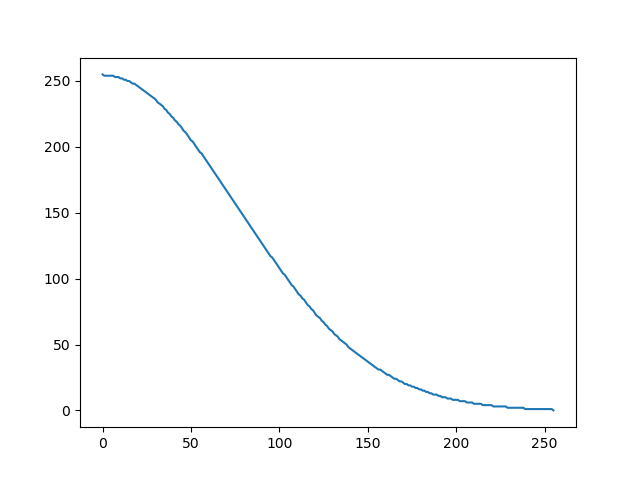
bilateralfilter()
今回は真面目に端っこのデータに対しても処理させるために、事前に画像をフィルタサイズ分大きくしておきます。画像の外の値に関しては、真面目に白を意味する255で埋めました。ただバイラテラルの性質として、自分の画素と遠い値は仲間外れにするので、255にする必要はないかもしれません。極端な話不定でもいいかも。そのうえで、実画像をその中心にはめ込む感じ。図にするとこんなイメージ。

フィルタの半径(size)分だけ四隅はみ出した画像を用意し、隅っこのフィルタ処理の際はそのはみ出した部分を参照するようにしてあげます。はめ込み自体は、大きな真っ白の画像(img_big)に対して、
img_big[size:-size-1,size:-size-1,:] = img #中心に画像をはめ込む
でコピーされるようです。恐ろしくらくちんです。メモリは倍使ってるんだろうけど。
続けて、フィルタサイズの分だけ、ループを回します。
まず、注目画素と周りの画素の差の絶対値を取り、その値をキーにして、色の差に応じた重みを保持するLUTを通します。こうして得られた重みを、今度は距離に応じた重み(gaus[x][y])に乗じてあげます。
dif = lut[abs(img - img_big[y:y-kernel_size,x:x-kernel_size,:])]
gau = gaus[x][y]*dif
こうして得られた重み(gau)が最終的にその画素に対して乗じる重みになるので、それを乗じてあげます。
sums += gau*img_big[y:y-kernel_size,x:x-kernel_size,:]
これを全画素に対して行うので、累積加算しています。
この時の重みは別途、最後加算値を正規化するために必要になるので、覚えておきます。
divs += gau
この処理をフィルタのカーネルサイズ分行い、最終的に正規化することで、結果を得ることができます。
まとめ
バイラテラルフィルタをPythonで、OpenCVを使わず記述してみました。それっぽい結果も出ているので、多分大間違いはしていないと思います。
OpenCVに頼りっきりにならないように、覚書として残しておきます。
追記
OpenCVのLUTを使ってたので、それも使わないようにしました。imread/imwriteだけOpenCV。


コメント