MTF測定用チャートに出てくるような同心円の画像を作る必要があったのでその過程を記しておきます。
仕様
任意のサイズ(正方形)の画像に対して、任意の個数の円を描画するもの。輝度変化はcosで変化し、円の外側は繰り返しにするか、指定の個数の円で打ち止めるか決められる。としました。
こんなのを発生させられるような関数。
コード
関数に切り出して、１０行で済んでしまいました。
1 2 3 4 5 6 7 8 9 10 11 12 13 | #### ２次元の同心円画像を発生def concentricCirclesGen(size, cycle, border=0): x = np.linspace(-cycle, cycle, size) xx,yy = np.meshgrid(x, x) dis = np.sqrt(xx**2 + yy**2) if border == 0: dis[cycle < dis] = cycle cos = (0.5*np.cos(2*np.pi*dis) + 0.5) * 255 return cos.astype(np.uint8) |
画像サイズの等差数列を作って、それを2次元に拡張。その差は円の個数で決定されます。3個の円を13×13画素で作りたければ、-3,-2.5,-2,…,2,2.5,3 という配列を作ることになります。これを2次元に拡張して2乗してルート。すなわち中心からの距離を表す2次元配列にします。
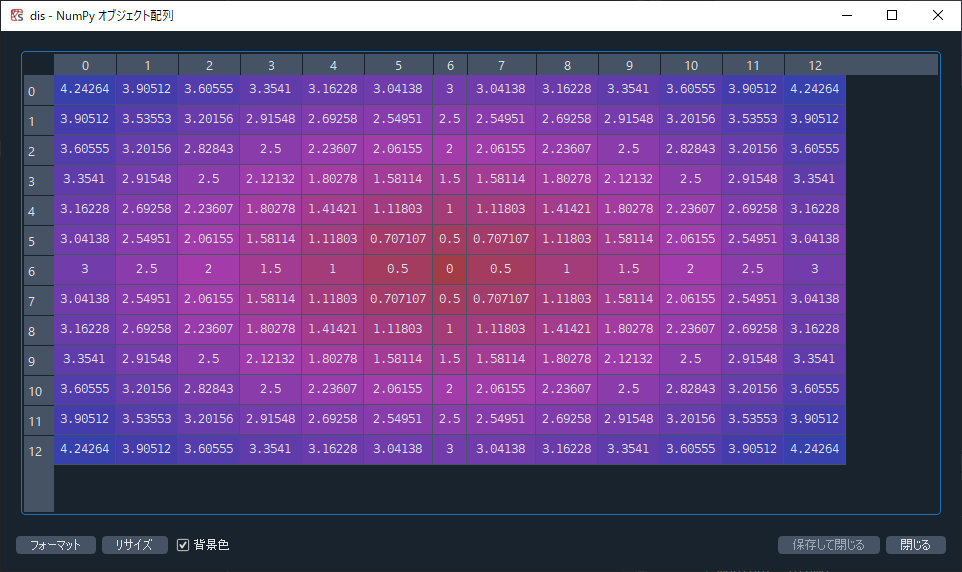
3より大きければ3にクリップすればそこより先の円は書かれません。これに2π掛けてcos通して0~255に正規化すだけ。
使い方は簡単。512×512、4個の円をきっかりで書きたければ
1 | img = concentricCirclesGen(512, 4) |
こんな呼び方で。
こんな画像が得られます。borderを非ゼロ指定すれば
1 | img = concentricCirclesGen(512, 4, border = 1) |
こう。cosの輝度変化が煩わしければ
1 | img = (img > 128) * 255 # 2値化 |
こんなして2値化すればよし。太さは2値化閾値（今回だと128）を調整すればよいです。
こう
たいしたもんではないですが、後でこの関数の書き方を忘れたとき用のメモですね。
コメント