SciPyには多くの窓関数が用意されています。有名なハミングの窓から何やら聞いたことのない窓まで。ただすべて1次元です。多分。
画像を扱うときには2次元で扱うことが多いのですが、どうにも2次元の窓関数が見当たらないのでSciPyで用意されている任意の窓関数を2次元に拡張する方法を考えてみます。
2次元ハニングの窓
2次元のハニングの窓を真面目にコーディングしてみます。中心からの距離に対して窓をかけるようなイメージです。
###
# sizeは窓の1辺の長さ。奇数
def han2d(size):
tap = size // 2
rad = np.linspace(-np.pi, np.pi, 2*tap+1) # -pi ~ pi
radx, rady = np.meshgrid(rad, rad)
radgrid = np.sqrt(radx**2 + rady**2) # 原点からの距離を示したグリッド
radgrid[radgrid > np.pi] = np.pi # piより大きいものはpiにクリップ(四隅)
han2 = 0.5 + 0.5 * np.cos(radgrid) # ハン窓の定義
これでなんとなく正しそうなハニングの窓(ハン窓)ができたような気がします。
ただこの要領で種類を増やそうと思うと、すべての窓関数の定義式を一つ一つトレースしないといけません。とてもめんどくさいです。
手を抜きます。
任意の窓関数の2次元化
1次元の窓関数をSciPyに作ってもらって、それを補間で2次元化します。中心からの距離を2次元のマップにして既存の1次元配列を参照すれば良いです。
size = 21
tap = size*2 # 元となる1次元配列は欲しいサイズの倍で作る
han = signal.hann(tap*2+1) # 1次元のハン窓
han = han[tap:tap*2] # 後ろの半周期取り出し
x = np.linspace(-tap, tap, size)
xx,yy = np.meshgrid(x, x)
mapx = np.sqrt(xx**2 + yy**2).astype(np.float32)
mapx[mapx > tap] = tap # 中心からの距離マップ
mapy = np.zeros_like(mapx) # 全マップ0
out = cv2.remap(han, mapy, mapx, cv2.INTER_LINEAR )
これでよいです。4行目の関数を好きな窓関数に差し替えれば、好きな2次元の窓関数が作れます。
mapxには中心からの距離が格納されているので、こんな感じです。ど真ん中が0で外に向かって中心からの距離にあたる値が入っています。

このマップの値に応じて、1次元のハン窓から線形補間して2次元化しているので、誤差はでます。
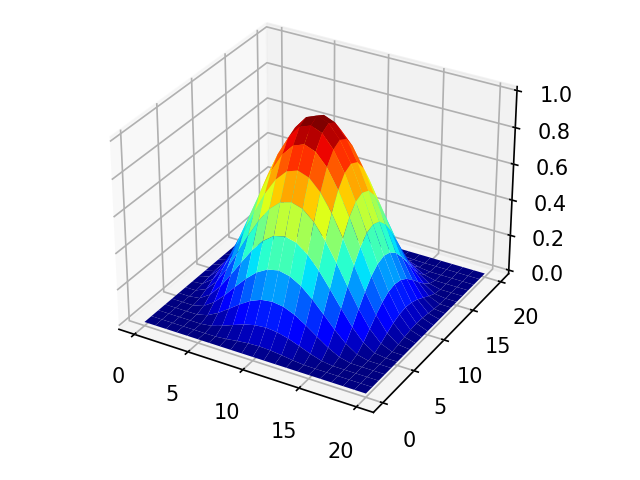
グラフからはわかりませんけどね。
先ほどの真面目に作った2次元ハン窓の関数との誤差を計算してみます
han2 = han2d(size)
maximum = np.max(np.abs(han2 - out))
この計算による最大誤差 0.000618920…です。(真面目に作った窓が正しいと仮定して)まぁ使用用途に寄りますが、一般的には許容範囲でしょう。
バリエーション
ハミングの窓
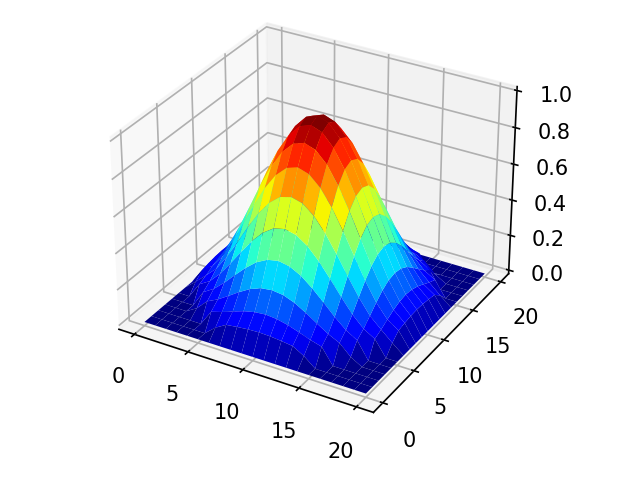
han = signal.hamming(tap*2+1)
ブラックマンの窓
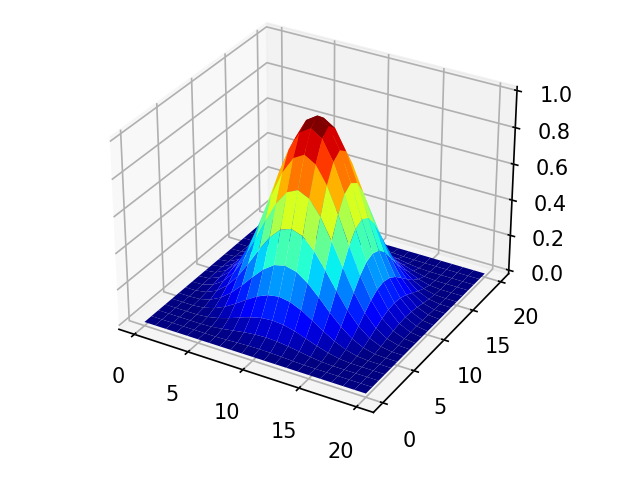
han = signal.blackman(tap*2+1)
矩形窓
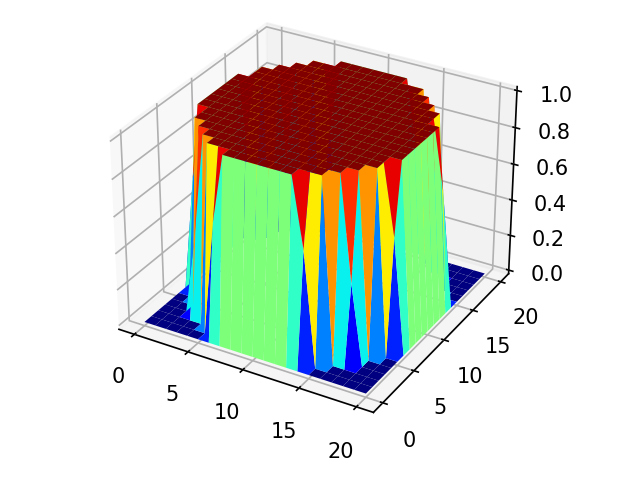
han = signal.boxcar(tap*2+1)
ガウシアン窓
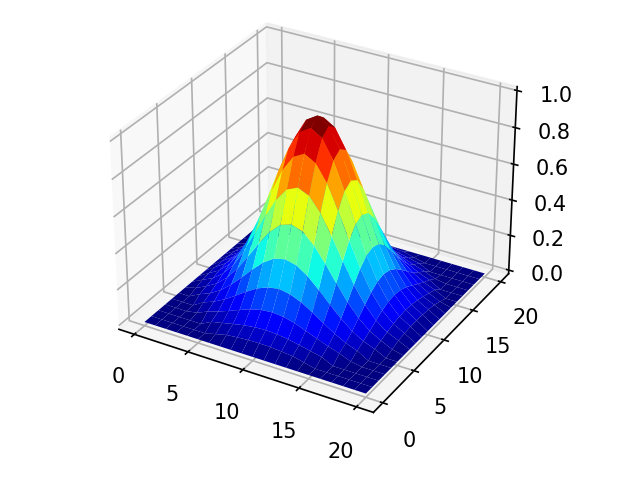
han = signal.gaussian(tap*2+1, 15)
好きなものを使うといい。
まとめ
1次元のデータ列さえあれば簡単に2次元化(近似)できる事がわかってしまいました。ややこしい計算はSciPyさんにお任せして、簡単に2次元への拡張されました。用途に応じて好きな窓が選べます。そんなに機会ないけど。
そして改めてOpenCVのremap関数はやはり大層便利な関数だということがわかりました。
remapの引数のbordermodeもREPLICATEが正しいのかなと思って試しましたが誤差変わらず。まぁこんなもんなのかな。


コメント