モルフォロジー変換と収縮・膨張の考え方はシンプルでわかりやすいのでまぁ詳細はいいとして、OpenCVのerodeとdilateの動きに関して確認してみました。Pythonで。
モルフォロジー変換
シンプルに膨張とか収縮とか言ってもらった方がしっくりきます。ややこしい言い方ですが、注目画素の値をWindow(kernel内の1の位置)内の最大値ないし最小値に置き換える処理です。
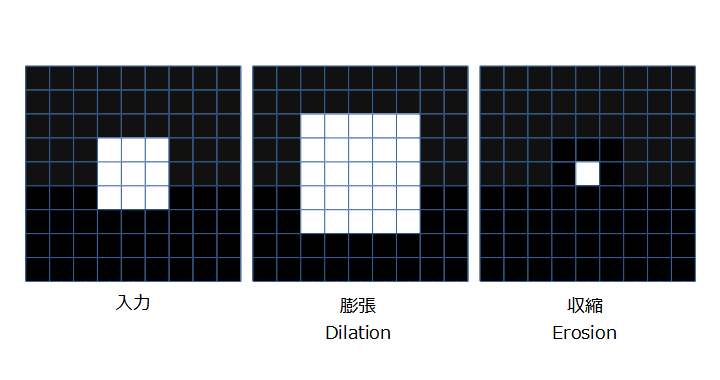
あたかも2値化後の画像処理のように思えてしまいますが、必ずしも2値画像を対象としてはいません。最大値や最小値を取るだけなので、多値画像に対しても処理が可能です。
ドキュメントにもあるように、OpenCVの関数ではその仕様になっているようです。律儀に最大値ないし最小値へ置き換えているようです。
入力画像
0/255または0/1の1chグレースケールの2値画像が入力だと思いきや、0~255の中間の値があっても良いし、RGB画像でもOKです。これもドキュメントに記載があります。
また8bitのunsigned int (uint8) だけかと思いきや、float64でもOKでした。かなり入力画像の幅は広いです。
収縮
最小値を取る方です。0が黒で255が白ならば白が縮む方向の処理です。この収縮の表現は白(非ゼロ)が主語のようですね。
関数の第二引数にkernelってのがあります。これがいわゆる窓で、1で埋まっている範囲で最小値を探します。
試しに3×3のkernelを使って、256×256のLenaの画像を収縮させると、
img = cv2.imread('Lena.png')
kernel = np.ones((3, 3), np.uint8)
erosion = cv2.erode(img, kernel, iterations = 1)

こんな感じ。わかりにくいので、以下のようなグラデーション画像(64×64)に対して5×5の収縮を行うと

全体が中心に向かって小さくなりました。
試してないけど膨張も同じ感じでしょう。
Kernelあれこれ
正方形
奇数×奇数の窓で、中心が注目画素。というのがオーソドックスな形でしょう。正方形かクロス、円形が基本形なのでしょう。
まず基本の正方形。5×5、3×3のオール1のkernelを用意してこの界隈でよく見るこんな画像に対して処理を施すと。
img = cv2.imread('j.png')
kernel = np.ones((3, 3), np.uint8)
erosion = cv2.erode(img, kernel, iterations = 1)
cv2.imwrite("errod3x3.png", erosion)
kernel = np.ones((5, 5), np.uint8)
erosion = cv2.erode(img, kernel, iterations = 1)
cv2.imwrite("errod5x5.png", erosion)

まぁ想定通りですね。今回この画像は2値画像ではなくあえて中間レベルもある画像を使っています。
3×3の窓使って、引数のiterationsってのを2にしてみると、5×5のiterations=1と同じ結果になりました。まぁこれも想定通りですね。適宜kernelサイズを変えるか、iterationsの回数を変えるか使い分けするんでしょうね。
縦横
次に縦長3×1と5×1のkernelを使ってみます。
img = cv2.imread('j.png')
kernel = np.ones((3, 1), np.uint8)
erosion = cv2.erode(img, kernel, iterations = 1)
cv2.imwrite("errod3x1.png", erosion)
kernel = np.ones((5, 1), np.uint8)
erosion = cv2.erode(img, kernel, iterations = 1)
cv2.imwrite("errod5x1.png", erosion)

これも想定通りですね。縦にだけ縮みました。丸が縦につぶれています。横も1×3、1×5で行えば同じ。
偶数
次に偶数を試します。4×4のkernelを使って収縮を行うとちょっと白の重心が右下にずれました。(画像を並べてもわかりにくいので画像は載せてませんが)5×5の最後の要素だけ0にした結果と同じになりますね。kernelサイズを2で割った座標が注目画素なのでしょう。きっと。
kernel = np.ones((4, 4), np.uint8)
erosion4 = cv2.erode(img, kernel, iterations = 1)
kernel = np.ones((5, 5), np.uint8)
kernel[:, 4] = 0
kernel[4, :] = 0
erosion5 = cv2.erode(img, kernel, iterations = 1)
このコードでいうところのerosion4とerosion5が同じ画像になります。

偶数の場合kernelの中心がずれるのでいまいちかもしれませんが、例えば1画素のノイズだけ消去したい(2×2は残したい)と思ったら2×2のkernelを使わざるを得ないですね。重心がずれることを考慮して使わないといけませんね。
目的に応じて偶数も含めて適切なkernelを作ってやる必要があります。
応用
ノイズに埋もれた縦の破線を膨張収縮だけで検出してみます。コードにするとこんな感じ。
kernel = np.ones((3, 1), np.uint8)
dilation = cv2.dilate(img, kernel, iterations = 2)
erosion = cv2.erode(dilation, kernel, iterations = 3)
output = cv2.dilate(erosion, kernel, iterations = 1)
縦長のkernelを用意して、2度の膨張、3度の収縮、1度の膨張を行うことで縦方向に連続している成分だけ残しています。2度のClosingを行った後に1度Openingを行っているのと同じですね。
こんなノイズ画像から縦線成分だけ取り出せています。

まずまずシンプルな処理でわかりやすい結果が出ています。
まとめ
処理としては単純でわかりやすいこの膨張と収縮。この関数をちょいと色々いじって遊んでみました。kernelの形を縦長や横長、偶数など色々試して結果をまとめてみました。
ノイズの形や大きさに応じてkernelの形、iterationsの回数を工夫することで色々使いでがありそうな感じです。



コメント