rawpyの現像関数、postprocessの引数であるgammaに関して、値の意味を確認していきます。
postprocessに関しての詳細はこちら。
gamma
通常入力された光量に対して、ディスプレイで観察するにふさわしい特性に変換するために、以下のようなガンマ補正が入っています。厳密にはディスプレイで人間が信号強度に線形性を感じられるように変換する。というのが正しいのかもしれません。
一般的には、1/2.2乗をかけるとかそんな言い方をする以下の式をよく見かけます。
$$out = in^{1/2.2}$$
ガンマそのものに関しては色々なサイトで説明があるので、詳細の説明はここでは割愛します。今回はこのpostprocess関数の引数で与えるgammaが何を意味しているのかを調べてみます。
BT.709
リファレンスによるとこのガンマ、値を2つ指定することになっています。デフォルトはBT.709にあたる(2.222, 4.5)とあります。パワーとスロープ(傾き)を指定することになっています。よく見る、上述したような単純な1/2.2ガンマではなさそうです。
このBT.709ですが、調べてみると、Rec.709という呼び方もされるようで、Wikipedia(英語)に詳しく解説がありました。とても全文を読む気にはなれませんでしたが、斜め読みしていくと、ガンマの説明があり、その中で、今回出てきた4.5という数字が表れました。
それを見ると、こんな式です。
$$V=\begin{cases}4.500L & L < 0.018\\1.099L^{0.45}-0.099 & L \geq0.0180\end{cases}$$
ダーク部の立ち上がりだけは、線形1次関数で与えられ、途中から見慣れたガンマのべき乗の関数に切り替わっています。今回のこれもおそらくこれを意味していると思われます。指数の0.45も何のことはない、逆数は2.222..なので、同じ意味です。
通常の1/2.2乗のガンマ(以降これを通常のガンマと呼びます。)も含めた3つのグラフを書いてみると以下のようになります。8binの入出力を想定した正規化を入れています。これを見ると通常のガンマ(グラフ黄色)が思いっきり急峻に立ち上がっているのがわかります。
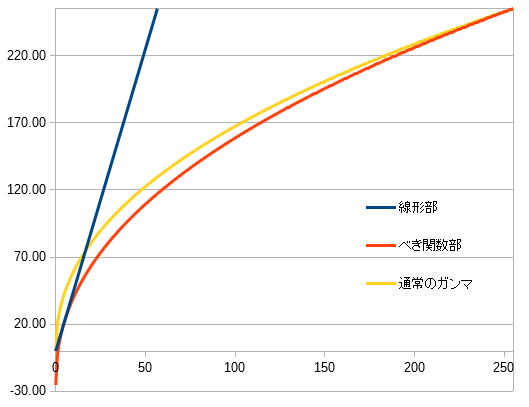
ダーク部だけ拡大したものがこれ、
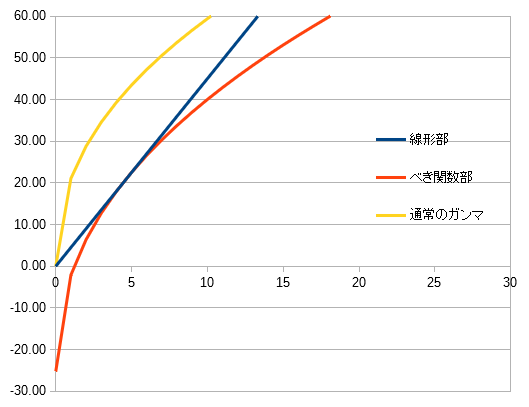
線形な箇所はもう少し立ち上がりが緩やかです。バトンタッチされたべき乗の関数部も、この線形部の傾きより緩やかになり始めているので、傾きは大きくないです。
詳しい理由を見つけることができなかったのですが、これはおそらく通常のガンマでは暗部のノイズを持ち上げすぎで、それを回避するための措置なのではないかと予想されます。
通常のガンマでは8bit換算で、1の入力に対して、出力が一気に21になります。2の入力で29。すなわち8bitの入出力処理系ではダーク部の1~20までの信号が失われていることになります。もちろんrawファイルには8bitを超えるデータが入っていると思われるので、ここまでひどくはないでしょうが。これはやりすぎ。
表にするとこんな感じ。色の切り替わりで関数が切り替わります。
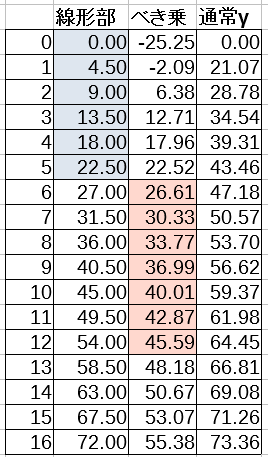
また当然暗部にはノイズも多く乗っています。それらも大きく持ち上がります。そんな当たりを勘案して、この最初線形、後からべき乗の関数。という落としどころをつけたのではなかろうか?と勝手に予想しました。
ただこの傾き4.5はどうやって決めたんだろうなぁ。べき乗の関数を微分した時に出てきた0.45をそのまま10倍した値。そして8bitの精度の入力で、 きれいに値が切り替わっている。(入力5の時の出力が22.5とほぼ同じ)何か意味があるのかな。
そしてこのパラメータがrawpy現像デフォルトになっていると思われます。
ただよくわからないのが、式にある、1.099とか0.099という値が、他のパワー、スロープの数値を入れた時にどのように変化するのか未確認です。きれいに接する(傾きが同じになる)点を見つけて、そこを交点に真面目に求めているのかもしれません。
実験
本当にrawpyで現像した画像が、このカーブに乗るのか確認してみます。手法としては、ガンマ1.0の画素値を横軸にして、デフォルトの画素値を縦軸にした散布図が先のグラフとマッチするか見てみます。
コードとしてはこんな感じ。Greenチャネルだけをプロットしています。力業です。全画素をプロットするので、メモリがっつり使う、それなりに重たい処理になります。
import rawpy
from matplotlib import pyplot as plt
import numpy as np
raw = rawpy.imread(filename)
ref = raw.postprocess(half_size=True,
use_camera_wb=True)
gam = [1.00,0.00]
img = raw.postprocess(half_size=True,
use_camera_wb=True,
gamma=gam)
plt.scatter(img[:,:,1], ref[:,:,1])
この結果描画されたグラフがこれ。一見すると、2.2乗のガンマと同じに見えます。
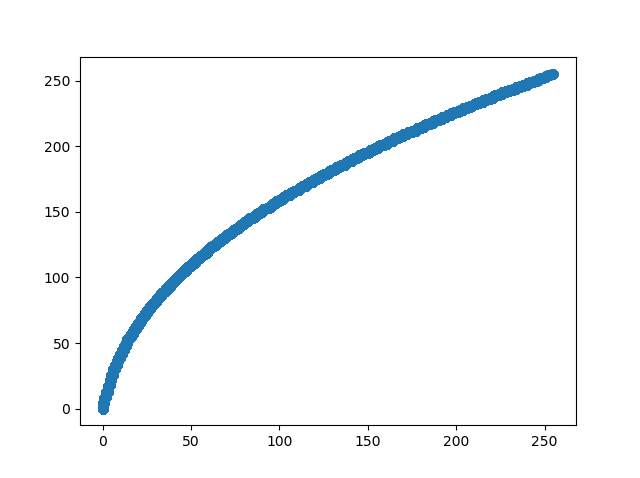
に対して、通常のガンマ配列と、0~5までを線形、6以降をべき乗の関数にしたBT.709の配列を作ってグラフを重畳させるとこんな感じ。
x = np.arange(0,256)
y = 255*np.power(x/255,1/2.222) #通常のガンマ
plt.plot(x,y,label="normal")
mid = int(255*0.018)
xx = np.arange(0,mid)
yy = 255*4.5*(xx/255) #0.018までの配列
xxx = np.arange(mid,256)
yyy = 255*(1.099*np.power(xxx/255,1/2.222) - 0.099) #0.018からの配列
x2 = np.concatenate([xx,xxx]) #結合
y2 = np.concatenate([yy,yyy])
plt.plot(x2,y2,label="BT.709")
plt.legend()
plt.show()
このコードの結果が以下。
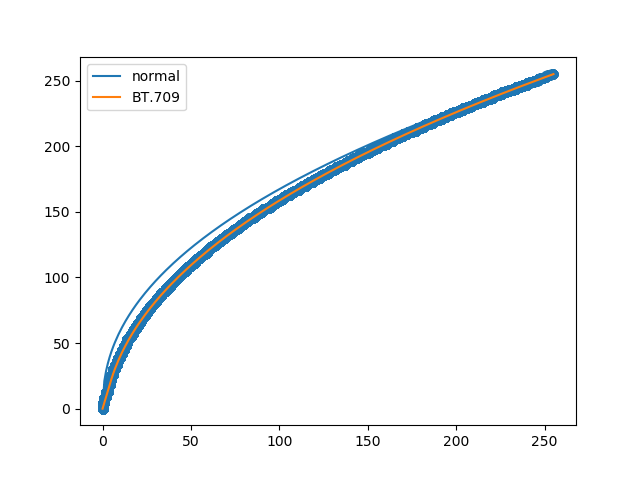
先の全画素プロットと完全一致しているように見えます。通常のガンマも合わせると、先のBT.709で観察したグラフと関係が一致しています。やっていることは見えました。
まとめ
一見小難しそうに見える、よく見るとなんて事の無いBT.709ガンマがrawpyデフォルトで使われていることが確認できました。
今回はあまり値を振りませんでした。またヒストグラムの変化もわかりにくいので、載せてません。せいぜいデフォルトかガンマ補正無しの1.0くらいしか使わないかなぁと思って。
以上。ガンマの調査でした。


コメント