線形回帰を行うとその直線の傾きがシンプルな式
$$a=\frac{v_{xy}}{v_x}$$
になることは以前式を展開して証明してみました。
なんとなく線形回帰は分布を最適に近似した直線だと思い込んでいましたが、この式を見るとその認識が間違っているということに気づきます。傾きの計算にy方向の分散が登場しないからです。
もしこの直線が分布を最適に近似しているのだとすると、xとyのデータを入れ替えてもその直線の傾きは変わらない(\(a\)の逆数になる)と思ってしまいますが、そうなりません。
少し詳しく見ていきます。
データを入れ替えた時の傾き
試しに適当なデータを作ってみます。エクセルで\(y=2x\)のデータと、それの\(x\)と\(y\)を入れ替えたデータを作ってグラフ(散布図)を書いてみます。そしてその近似直線を表示させます。すると

こんな感じ。想像通り傾きは2とその逆数の0.5になります。軸を入れ替えているので当たり前です。(切片に極小さいゴミが乗っかってますが)
続いてここで適当な乱数\(\alpha\)を加算して\(y=2x+\alpha\)にして同じようにグラフを書いてみます。
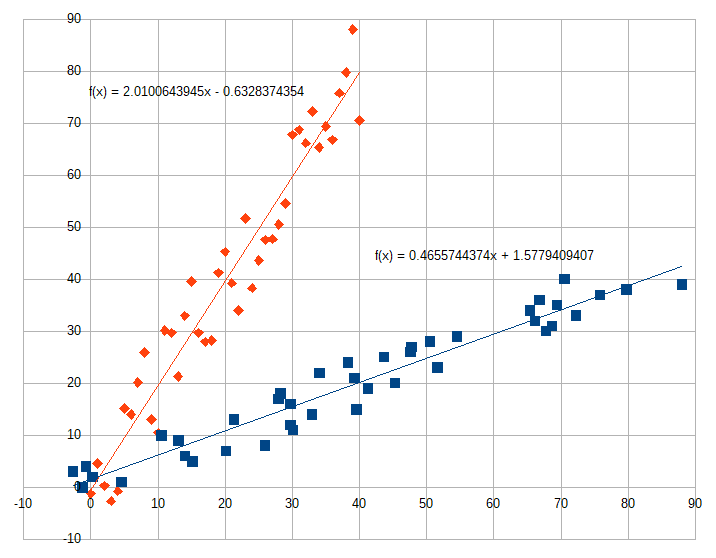
するとそれぞれの傾きが、2.010と0.466になり、逆数の関係ではなくなってしまいました。切片もそれなりに大きい値になり、原点でクロスしません。
しっくりきません。分布を表現する最適な直線を書いているはずなのに…。と思ってしまいます。
二乗誤差最小の定義
これは別に計算誤差ではありません。正しい計算結果です。
冒頭に示した、回帰直線の傾きを求める式を見ると
$$a=\frac{v_{xy}}{v_x}$$
となっています。この式の\(x\)と\(y\)を入れ替えると式は、
$$a’=\frac{v_{xy}}{v_y}$$
となるだけで、この\(a\)と\(a’\)が逆数になることなんぞ保証されません。x’の分散とy’の分散は基本的に独立なので。もう少し考えてみます。
この式を求めた時の定義に立ち返ります。この式の前提は、\(y=ax+b\)の二乗誤差を最小にする。という問題を解いた結果です。式で書くと
$$Err=\sum_i^n(ax_{i}+b-y_{i})^{2}$$
の値を最小にする\(a\)を求める問題を解いただけです。この\(Err\)が意味するのは\(y\)の最小値です。\(x\)には誤差がないことを前提にしています。(実際データもそうやって作っています)図にすると
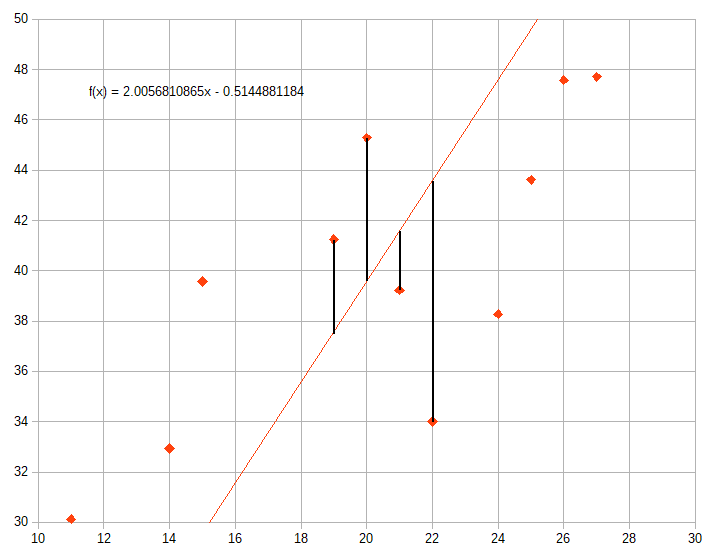
この黒線の長さ(厳密にはこの黒線を1辺とする正方形の面積)を最小にするのであって、直線までの距離を最小にしているわけではありません。
つまり
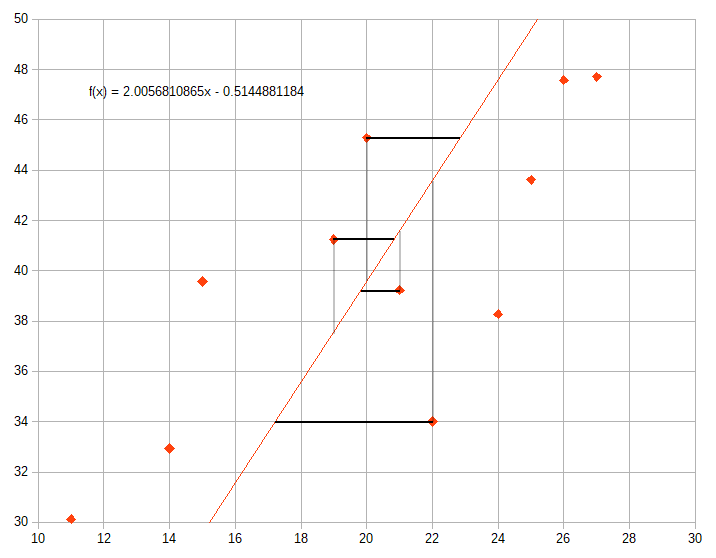
この横方向の長さなんぞ知ったことはないのです。これが軸を入れ替えた時に傾きが逆数の関係にならない理由です。多分。
なので軸の取り方は気を付けないといけません。x方向には誤差がないデータをyには誤差を含んだデータを並べることで回帰直線を求めることが必要です。
例えば…7月の毎日決まった時間の気温。であればx方向に時間、y方向に気温を取ることで、8月の気温が想像できる。とか。多分そんな使い方です。
例えば以下の表の様なクラスの生徒の国語の点数、算数の点数をプロットすると
| 生徒 | 国語 | 算数 |
| a | 80 | 90 |
| b | 70 | 60 |
| c | 90 | 70 |
| d | 20 | 40 |
| e | 30 | 60 |
| f | 50 | 40 |
| g | 30 | 30 |
| h | 40 | 20 |
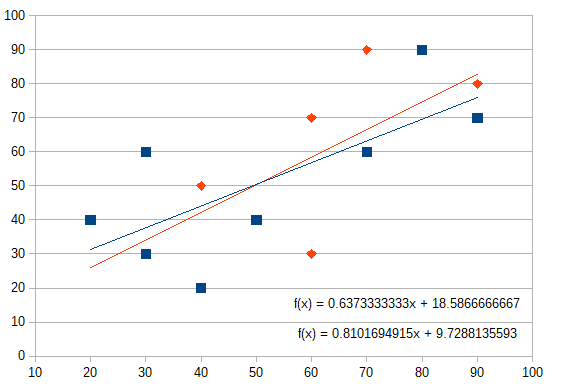
青点がx方向に国語y方向に算数をプロットしたもの。オレンジ点がその逆でプロットしたものです。それぞれ回帰直線を引いてみるとこんな感じで、例えば国語の点数が80点だったら算数は何点でしょう?を求めるのは青の線でみて約70点。では逆に算数が70点だったら国語は何点でしょう?を求めるのはオレンジの線で約65点。集団が大きくなればこの2つくらいは相関出てくるのかもしれませんが、軸が変わると傾きが変わることは気にしておく必要があります。
まとめ
通常の線形回帰で得られた直線の傾きは、xとyのデータを入れ替えても逆数の関係にはなりません。
x方向のデータ(説明変数というらしい)には誤差がないものを、y方向のデータ(目的変数というらしい)に誤差を含むものを取ることを前提としているようです。なので両方に誤差を含むようなサンプルには適さないようです。両方に誤差を含む分布に対する特殊な回帰もあるようですが、今回はそこまでは突っ込みません。
軸の使い方と、プロットするサンプルと近似の方法はちゃんと意味を考えないといけないなぁ~。


コメント