共分散を使って最小二乗を解き直線近似してみる

　以前行列を使って最小二乗による線形回帰の解き方について考えてみましたが、1次の関数への近似であれば分散使ってもう少し簡単に計算ができてしまいます。今回は分散と共分散を使って求める方法に関して試してみます。

　最小二乗により求まった直線の傾きは共分散を分散で割ったものだそうです。

$$a=\frac{v_{xy}}{v_x}$$

　式だけ眺めてもふーんそんなもんなんだ、で終わってしまうのでちゃんとゴリゴリ解いてみます。

　式はたくさん出てきますが丁寧に展開しているだけなので追っかけるのはさほど難しくはないと思います。

最小二乗法による1次直線フィッティング
平均
分散
共分散
計算の続き

最小二乗法による1次直線フィッティング

　冒頭は以前の記事の焼き増しです。まずは$\sum$を使って最小二乗の式を解いてみます。1次関数なので、フィッティングする式は

$$y=ax+b$$

　になります。この $x$と$y$がデータとして複数($N$個)あるとします。このデータを上記式にフィッティングさせます。この時発生する誤差$Err$の二乗和を最小にするので、

$$Err=\sum_i^n(ax_{i}+b-y_{i})^{2}$$

　を最小にすればよいです。泥臭く展開します。

$$Err= \sum_i^n(a^{2}x _{i} ^{2}+2abx _{i} -2ax _{i} y _{i} -2by _{i} +b^{2}+y _{i} ^{2})$$

　今回は最終的に、$a$と $b$ を求める問題なので、 $a,b$が変数で、 $x,y$が定数になります。ここで$a$に着目すると、 $Err$を最小にする際に $b$ は直接関係ない。なので、 $b$も$a$にとっては定数。

　というわけで、$a$を変数とした式としてみると、ただの下に凸の2次関数であることがわかります。結果の最小値を求めるには、偏微分して、極値を求めればよい。

　というわけで、偏微分してみます。

$$\frac{\partial}{\partial a}\sum (a^{2}x_{i} ^{2}+2abx_{i} -2ax_{i} y_{i} -2by_{i} +b^{2}+y_{i} ^{2})$$

$$=(2a\sum x^2_{i}+2b\sum x_{i}-2\sum x_{i}y_{i})$$

　まだ$\sum$が残ります。この結果が0になる時の$a$なので、最終的には、

$$a\sum x^2_{i}+b\sum x_{i}=\sum x_{i}y_{i}$$

　となります。同様に$ b $に関しても偏微分して解くと、

$$a\sum x_{i}+b\sum １=\sum y_{i}$$

　同じような式になります。これはただの連立方程式です。ここから行列を使って解いたのが前回のパターン。

　今回は連立方程式を使って解いていきます。

　そこでまずシグマの変形のためにまず平均、分散、共分散の定義を見ていきます。

平均

　これは簡単ですね。すべてのサンプルを足してサンプル数Nで割ったものです。なので平均$\mu$は

$$\mu_x=\frac{1}{N}\sum_{i=1}^N{x_i}$$

$$\mu_y=\frac{1}{N}\sum_{i=1}^N{y_i}$$

　なので、結果として$\sum$の部分は

$$N\mu_x=\sum_{i=1}^N{x_i}$$

　となります。

分散

　これもさほど難しいものではないですね。散らばり度合を意味しています。値が大きいほど分布は広がってることになります。すべてのサンプルに対して平均との差の二乗を合計して、やはりNで割ったものです。式にすると分散$v$は

$$v_x=\frac{1}{N}\sum_{i=1}^N(x_i-\mu_x)^2$$

　です。展開します。

$$\frac{1}{N}\sum_{i=1}^N(x_i^2-2\mu_xx_i+\mu_x^2)=\frac{1}{N}\sum_{i=1}^Nx_i^2-2\frac{1}{N}\sum_{i=1}^N\mu_xx_i+\frac{1}{N}\sum_{i=1}^N\mu_x^2$$

　先ほどの平均の定義より真ん中の項は

$$-2\frac{1}{N}\sum_{i=1}^N\mu_xx_i=-2\mu_x\frac{1}{N}\sum_{i=1}^Nx_i=-2\mu_x^2$$

　また最後の項も

$$\frac{1}{N}\sum_{i=1}^N\mu_x^2=\mu_x^2\frac{1}{N}\sum_{i=1}^N1=\mu_x^2\frac{1}{N}N=\mu_x^2$$

　となりますので、分散の式はシンプルに

$$v_x=\frac{1}{N}\sum_{i=1}^{N}x_i^2-\mu_x^2$$

　となりやはり$\sum$の部分は

$$N(v_x+\mu_x^2)=\sum_{i=1}^{N}x_i^2$$

　となります。二乗の平均から平均の二乗を引くと分散になるんですね。初めて気づいた。

共分散

　　最後に共分散です。これはなかなか一言では説明できないです。自分も使いこなせてませんし。

　二つの分布の相関を出すときとかに使います。2つの変数の偏差の積の平均です。絶対値が大きいほど2つの変数の相関が強く、小さいほど相関が低くなります。定義は

$$v_{xy}=\frac{1}{N}\sum_{i=1}^{N}(x_i-\mu_x)(y_i-\mu_y)$$

　です。すべてのサンプルの偏差同士を乗じ、その合計をやはりNで割ったものです。

　この意味を少し突っ込んで考えてみます。以下のようなデータ列$x_i$と$y_i$があった場合、その平均と平均との差分を意味する偏差は以下の表の様になります。

$i$	$x_i$	$y_i$	$x_i$の偏差	$y_i$の偏差
0	0	0	-4.5	-4.5
1	1	1	-3.5	-3.5
2	2	2	-2.5	-2.5
3	3	3	-1.5	-1.5
4	4	4	-0.5	-0.5
5	5	5	0.5	0.5
6	6	6	1.5	1.5
7	7	7	2.5	2.5
8	8	8	3.5	3.5
9	9	9	4.5	4.5
平均	4.5	4.5

　なのでこの偏差同士の積の平均なので、この分布の共分散は8.25となります。かなり強い正の相関がある。とみるようです。平均近くは小さいもの同士、平均から遠いものは大きいもの同士の積を取るので値は大きくなっていきます。片方が平均から遠い時他方も遠い。片方が平均付近なら他方も平均付近。というこのような分布であれば値が大きくなっていきます。

グラフにするほどでもないですが以下のような感じ

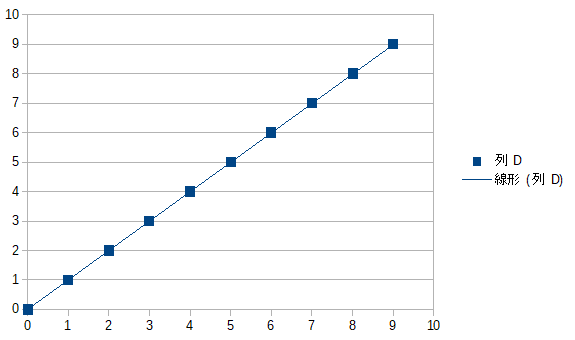
　では同じように0~9の値を1回ずつとる別の分布$y’_i$、を考えてみます。同じ値を同じ回数だけ取るので、$y’_i$単独で考えれば平均も分散も先の$y_i$と同じですが、共分散が大きく異なります。

$i$	$x_i$	$y’_i$	$x_i$の偏差	$y’_i$の偏差
0	0	4	-4.5	-0.5
1	1	6	-3.5	1.5
2	2	2	-2.5	-2.5
3	3	8	-1.5	3.5
4	4	0	-0.5	-4.5
5	5	9	0.5	4.5
6	6	1	1.5	-3.5
7	7	7	2.5	2.5
8	8	3	3.5	-1.5
9	9	5	4.5	0.5
平均	4.5	4.5

　この共分散は0.05となり、ほぼ相関なし。という分布になります。先ほどとは対照的に片方が大きい偏差を持つ時に他方が小さい偏差を持っているのでその積は小さくなります。その平均なので値は小さくなります。グラフにしてもまぁそりゃ相関ないですな。

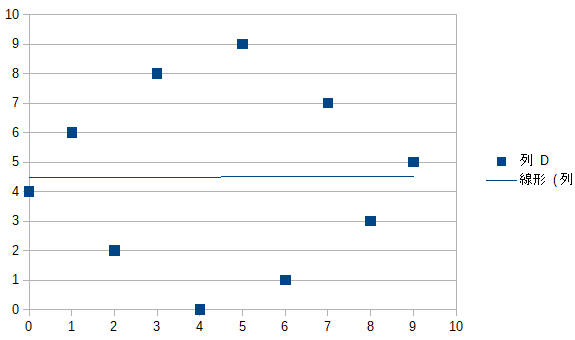
　共分散がいくつなら相関ありで、いくつから相関なしとみるかは難しく、この共分散をそれぞれの標準偏差の積で割った相関係数の大小で相関を判断するのが一般的なようです。が今回はそこまでは突っ込みません。あくまで最小二乗を解くために共分散を使うと便利だ。というところまで。

　こんな共分散ですが、定義の式をまたゴリゴリ展開していきます。

$$v_{xy}=\frac{1}{N}\sum_{i=1}^{N}(x_i-\mu_x)(y_i-\mu_y)=\frac{1}{N}\sum_{i=1}^{N}(x_iy_i-\mu_yx_i-\mu_xy_i+\mu_x\mu_y)\\=\frac{1}{N}\sum_{i=1}^{N}x_iy_i-\frac{\mu_y}{N}\sum_{i=1}^{N}x_i-\frac{\mu_x}{N}\sum_{i=1}^{N}y_i+\frac{1}{N}\sum_{i=1}^{N}\mu_x\mu_y$$

　なのでそれぞれの項は

$$\frac{\mu_y}{N}\sum_{i=1}^{N}x_i=\mu_y\mu_x\\\frac{\mu_x}{N}\sum_{i=1}^{N}y_i=\mu_x\mu_y\\\frac{1}{N}\sum_{i=1}^{N}\mu_x\mu_y=\mu_x\mu_y\frac{1}{N}\sum_{i=1}^{N}1=\mu_x\mu_y\frac{1}{N}N=\mu_x\mu_y$$

　となり、結果はまたもシンプルに

$$\frac{1}{N}\sum_{i=1}^{N}x_iy_i-\mu_x\mu_y-\mu_x\mu_y+\mu_x\mu_y=\frac{1}{N}\sum_{i=1}^{N}x_iy_i-\mu_x\mu_y$$

　となります。それぞれの積の平均から平均の積を引くと共分散です。

$$v_{xy}=\frac{1}{N}\sum_{i=1}^{N}x_iy_i-\mu_x\mu_y\\N(v_{xy}+\mu_x\mu_y)=\sum_{i=1}^{N}x_iy_i$$

　ここからも$\sum=$の形が作れました。

計算の続き

　ここまでで、平均と分散と共分散の3つを使ってシグマのすべてが置き換えられます。これらを元の式のシグマに代入します。

$$a\sum x^2_{i}+b\sum x_{i}-\sum x_{i}y_{i}=0$$

$$a\sum x_{i}+b\sum １-\sum y_{i}=0$$

　これまでの苦労のかいがあり、めでたくシグマが消えます。

$$aN(v_x+\mu_x^2)+bN\mu_x-N(v_{xy}+\mu_x\mu_y)=0\\aN\mu_x+bN-N\mu_y=0$$

　$N$も消えます。

$$a(v_x+\mu_x^2)+b\mu_x-(v_{xy}+\mu_x\mu_y)=0\\a\mu_x+b-\mu_y=0$$

　$\mu_x$を下の式に掛けて$b$を消します。

$$a(v_x+\mu_x^2)+b\mu_x-(v_{xy}+\mu_x\mu_y)=0\\a\mu_x^2+b\mu_x-\mu_x\mu_y=0$$

　全部展開して上の式から下の式を引きます。

$$av_x+a\mu_x^2+b\mu_x-v_{xy}-\mu_x\mu_y=0\\a\mu_x^2+b\mu_x-\mu_x\mu_y=0$$

　恐ろしくシンプルな$a$だけの式になります。

$$av_x-v_{xy}=0$$

$$a=\frac{v_{xy}}{v_x}$$

　同様に$b$は

$$b=-a\mu_x+\mu_y = \mu_y-\frac{v_{xy}}{v_x}\mu_x$$

　この式$a\mu_x+b=\mu_y$なので、最小二乗により求めた直線は平均を通る。ということを示しています。

　これにて計算終わり。冒頭で述べたように最小二乗により求めた1次関数の傾きは共分散を分散で割ることで求まることが導けました。

　色々小難しそうな定義やら式でしたが、解いてみると恐ろしくシンプルな式で傾き$a$が求まりました。つまりある分布を1次関数に近似させるとその直線は$x$の分散だけ$x$方向に進んだのちに$xy$の共分散だけ$y$方向に進むということになります。少なくとも式の意味はそうです。$y$の分散が登場しないことに若干の違和感を残しながらもいろいろなところで見かける式が導出できたのでひとまずよしとします。

　追記：違和感の理由はわかりました。データのｘとｙを入れ替えた時に同じ直線に近似されないからですね。