離散フーリエ変換を心で理解する

　道具として使う場面が多いフーリエ変換ですが、式を見るとやれeだの複素数だの、こちらの理解を放棄させてくれます。使う以上意味を理解しようと思い、離散フーリエ変換の式の意味を少し考えてみます。厳密さは問わない事にします。

　色々悩み至った結論は

　・異なる周期の波同士の積の和はゼロになる。

すなわち

　・同一周期の波同士の積の和でその周期のパワーがわかる。

　これを確認していきます。

フーリエ級数展開
フーリエ級数の求め方
離散フーリエ変換
まとめ

フーリエ級数展開

　ある任意の関数が色々な周期のcos/sin関数の重ね合わせで実現できる。というざっくりとした理解でひとまず先に進みます。

　式としては

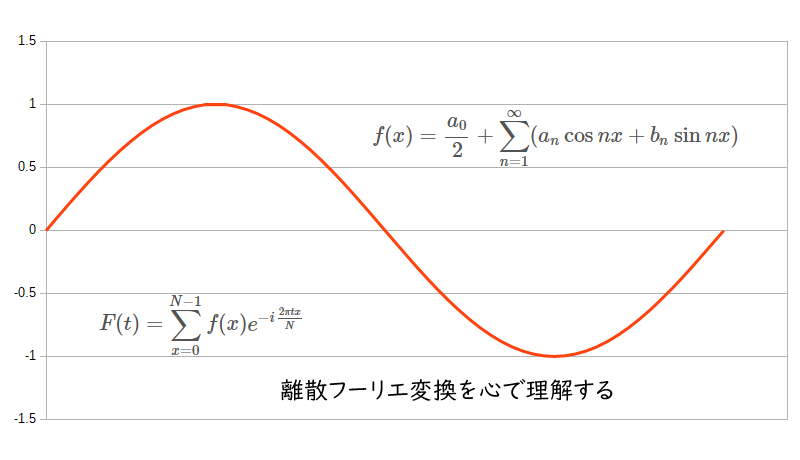
$$ f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty(a_n\cos nx + b_n \sin nx) $$

　こんな感じ。定数部は厳密性は捨てます。

　しかしながら一般的に（特にフーリエ変換の式）式にcos/sinが出てこず、eでまとめられています。しかも複素数。

$$ f(x)=\sum_{n=-\infty}^\infty c_n e^{-inx} $$

　まずこれで意味が分からなくなりますが、何のことは無い同一周期のcos/sinが出てくるのが邪魔くさいと考えた誰かがオイラーの公式でひとまとめにしただけです。

$$ e^{i\theta} = \cos \theta + i\sin \theta $$

　オイラーの公式に関してはこれ以上突っ込んで説明はしません。こんなものだと思っておくことにします。それほど難しい証明では無いのでWebサイトを斜め読みしてもなんとなく理解した気になれます。

　ここはまだ理解可能です。ただ個人的には複素数の実部でcos、虚部でsinというのが分かりにくいのでcos/sinのままにしときます。

　これだけの事なのでeや複素数があってもさほどビビることはない。

フーリエ級数の求め方

　式です。

$$ a_0 = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)dx \\
a_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nx dx \\
b_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nx dx $$

　かなりシンプルです。$a$と$b$の違いはcosかsinだけの違いです。この式にて任意の関数のとある周期$nx$の強度が計算できるということです。本当か？定数の1/πの部分はひとまず置いといて、なぜこれでとある周期$nx$の波の強度がわかるのか考えてみます。

　式を見るとある関数$f(x)$に対して求めたい周期$nx$のcosを乗じてそれを-πからπまで積分しています。

　例えばとある関数が定数aだとすると、cosを乗じた結果は振幅aのcosになるだけで、1周期積分すると面積はゼロです。当然$n$周期にあたる-πからπまで積分してもゼロ。つまりこのとある関数$f(x)$には周期$nx$のパワーがまったく無いということになります。当然です。定数aなので直流成分しかありませんから。

　ではとある関数$f(x)$が周期$m$で構成されているとします。するとこの式は$cosmx$と$cosnx$の積で表され、積和の公式より、2つのcosの和に変換されます。

$$ \cos mx \cos nx = \frac{1}{2}\left\{\cos(mx+nx) + \cos(mx – nx )\right\} $$

　これを同様に-πからπまで積分するとゼロになります。m=nの時以外では。

　つまりこの式で$\cos n$の周期以外の波の成分はゼロになり、$n$の周期を持つ波だけ値を持つことができます。

　積和の公式を見るとsinも同様です。同一周期のsinの積以外では積分した値が必ずゼロになります。

　cosにsinを乗じた場合は同じ周期でもゼロです。同じ周期、同じ位相の波同士の積でないと必ず積分した値がゼロです。（位相のずれも位相ゼロのcosとsinに分解できるのでそれぞれパワーが出ます。）

　直感的にもなんとなくわかります。違う周期の波を掛け合わせたら平均はゼロになりそうですが、同じ波なら符号が逆に向くことが無く値が出そうです。

　グラフにしてみるとなんとなくわかった気になります。ベースとなる4周期の赤のcosカーブに対して、黄色のカーブを1~6周期分用意し、その両者の積を取ったものを緑でプロットしています。

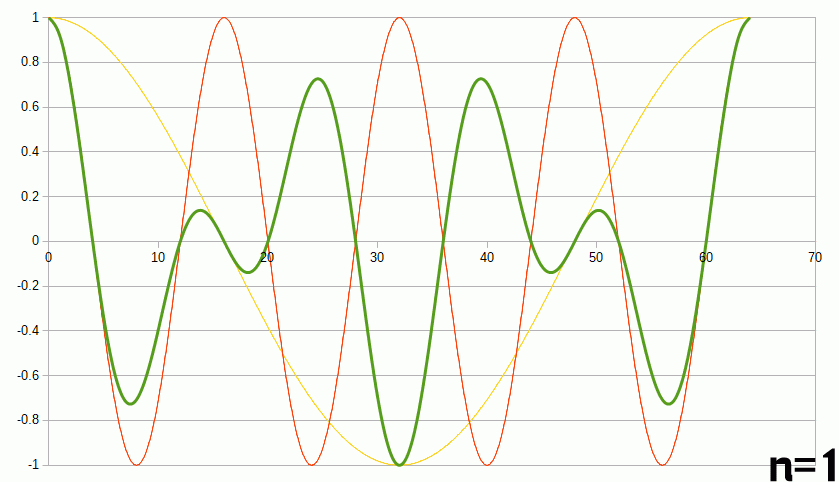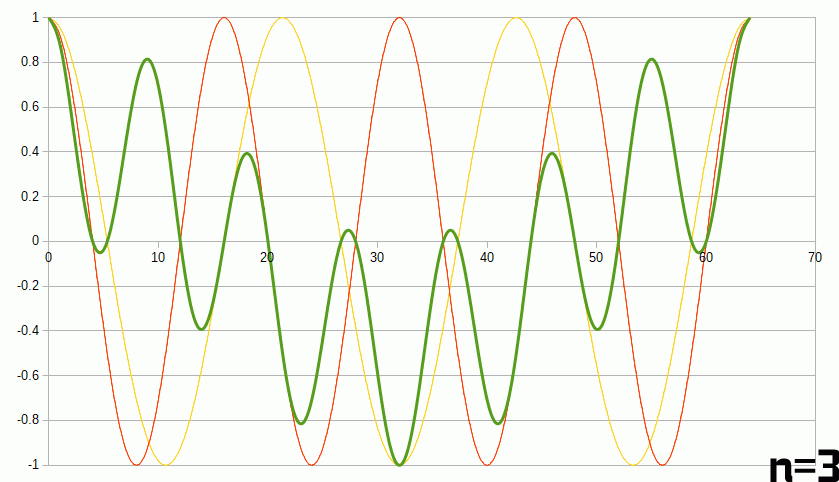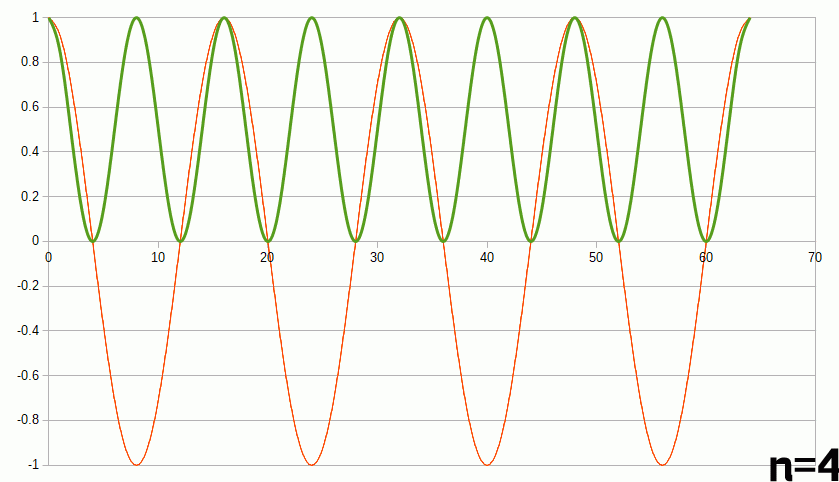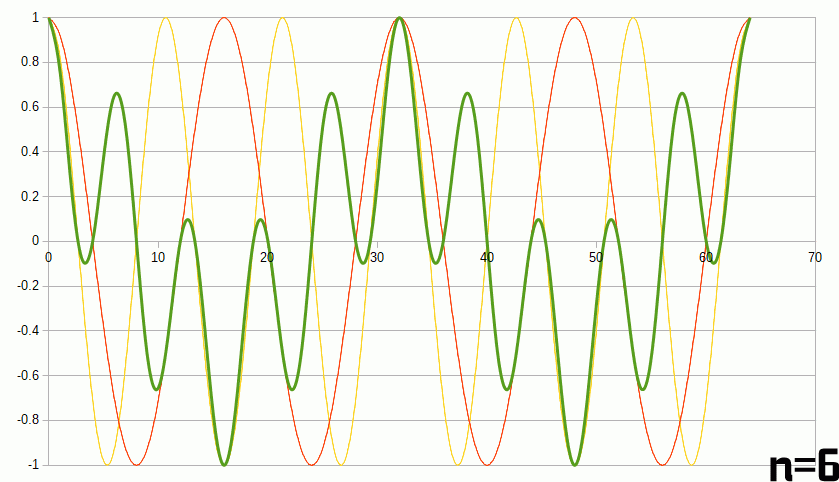
　n=4の時すなわち黄色と赤のカーブが一致した時にだけ緑のグラフが片側にそろいます。逆にそれ以外の時は正と負の値で打ち消しあって面積がゼロになってしまいます。上の式でいうところのm=nの時以外で積分ゼロはこんなところからも想像できます。sinでも同じだし、n=3同士でも同様です。

　このnを1～∞まで変化させればすべての周期のcos/sinのパワーがわかりそうです。任意の波形がcos/sinの合成で表現できている限り。

　一般的にこれは関数の直交性とかって呼ばれるらしいです。

離散フーリエ変換

　通常はここからフーリエ変換の話に進むのだと思いますが、すっ飛ばします。むしろこの級数展開の式からの方が離散フーリエ変換の式は理解しやすい気がしています。

　離散フーリエ級数展開ととらえた方がプログラムも書きやすいです。

　式です。

$$ F(t)=\sum_{x=0}^{N-1}f(x)e^{-i\frac{2\pi tx}{N}} $$

　やはり複素数はよくわからないのでオイラーの公式使って

$$ F(t)=\sum_{x=0}^{N-1}\left\{f(x)\cos{\frac{2\pi tx}{N}}+ f(x)\sin{\frac{2\pi tx}{N}} \right\} $$

　とある周期tに着目すると同じように関数$f(x)$に周期tのcosを乗じたものを分解能Ｎで1周期分積分してます。tを0から順に欲しい解像度（通常はナイキスト、サンプリング周期の半分）まで順繰りに計算すればよい事になります。

　tが1の時は一番ゆっくりとした波と解析したいデータ列との積を1周期分
　tが2の時は倍周期の波と解析したいデータ列との積を2周期分
　それぞれ和を取っていけばよいことになります。

　プログラムっぽく書くと

for(t=0;t<N/2;t++){
	Fc[t] = 0;
	Fs[t] = 0;
	for(x=0;x<N;x++){
		Fc[t] += data[x] * cos(2*pi * t * x/N);
		Fs[t] += data[x] * sin(2*pi * t * x/N);
	}
}

　tのループが周期（周波数）、xのループがサンプル数（解像度）。コードを眺めた方が式を眺めるより理解できるのは私だけでしょうか…？