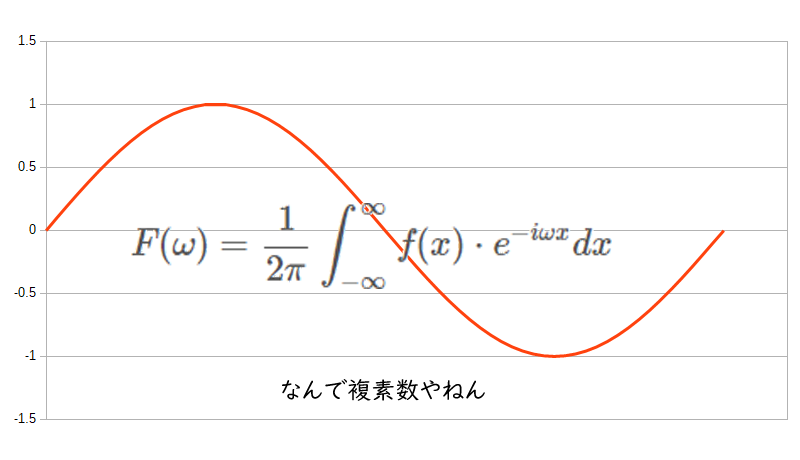
道具として使う場面が多いフーリエ変換ですが、式を見るとこちらの理解を放棄させてくれます。特に虚数部。なんで複素数やねん。
フーリエ級数展開まではまぁまだ良いです。
色々な周期のcos/sinの可算で任意の関数が表現できるってのはまだ理解できます。
じゃあなぜ突き詰めると複素数になるのかそのあたりを考えてみます。かなり乱暴な記事なので間違いあったらごめんなさい。厳密性は勘弁して下さい。イメージです。
結論から言うととある周期とそれに対する位相のずれを表現する手段として複素数が便利だった。って事のようです。
フーリエ級数展開とフーリエ変換
少し前まで自分はフーリエ級数展開とフーリエ変換の決定的な意味の違いを理解できていませんでした。フーリエ変換はフーリエ級数展開の発展版くらいで考えていました。
全然違います。左辺が違います。
フーリエ級数展開
フーリエ級数あくまで級数展開なので左辺が元の式で、それを他のシンプルな式の足し算で表現した式です。テイラー展開とか、その親戚です。
$$ f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty(a_n\cos nx + b_n \sin nx) $$
フーリエ変換
対してフーリエ変換は、任意の式がcos/sinで表現できるんなら、cos/sinの周期を変数とした関数へ変換できるんじゃないか?って事で生まれた変換です。フーリエ級数展開のa,bの級数を変数とした関数に変換してやろう。って事です。
$$ F(\omega) = \frac{1}{2\pi}\int_{-\infty}^{\infty} f(x)\cdot e^{-i\omega x}dx $$
なので左辺が変換後の周波数を変数とした関数になります。一般的には時間軸から周波数軸への変換。とかそんな言われ方するのはフーリエ変換の方。関数の展開では無いです。
ちなみにcos/sinが消え去って見えるのはオイラーさんの仕業です。しっかり存在します。
フーリエ変換したら色々便利だった。ってことで広く応用されているって事だと思います。
複素数
じゃあなんでフーリエ変換した結果が複素数やねん。周波数空間じゃないんかい。と思ってしまいます。
フーリエ変換した結果も通常周波数スペクトルで可視化することが多いですし。虚数じゃないじゃん。と不思議に思ったものです。
ただcosとsinに分解したのに、値がスペクトル一つってのがおかしいわけで、cosとsinのパワーそれぞれあるはずです。cos/sinで考えると周期とパワーしか無いように見えますが、実は位相の成分が隠れています。
周波数空間への変換と名乗っているものの、位相のずれ量が無いと元の関数に戻せません。
例えば\(a\cos (\theta )\)と\(a\cos (\theta + \phi)\)は同じ周波数の関数で、パワーは同じですが、同じ変換がされるようではフーリエ逆変換で元に戻せません。
先の\(a\cos (\theta + \phi )\)は加法定理でsinとcosの和で表せます。
$$ a\cos(\theta + \phi) = a\cos(\theta)\cos(\phi) – a\sin(\theta)\sin(\phi) $$
\(\cos(\phi)\)と\(\sin(\phi)\)は定数なので、cosの位相のずれ\(\phi \)は同一周期\(\theta \)のsinを加算することで表現できるという事になります。
試しにとある振幅1周期1と振幅0.5周期3のcosを加算した信号に対して、徐々に位相をずらしてフーリエ変換してみます。
$$ sig(x) = \cos(x + \phi) + 0.5\cos(3x + \phi) $$
pythonで書くとこんな感じ。
N = 32 # データ数
n = np.arange(32)
for i in range(32):
phi = np.pi*i/32
signal = np.cos(2*np.pi*n/N + phi) + 0.5*np.cos(3*2*np.pi*n/N + phi)
F = np.fft.fft(signal) # 高速フーリエ変換(FFT)
amp = np.abs(F/(N/2)) # 振幅
plt.plot(F.real[:N//2]*2/N, label="cos")
plt.plot(-F.imag[:N//2]*2/N, label="sin")
plt.plot(amp[:N//2], label="amplitude")
この\(\phi\)を徐々にずらした関数をfftしたグラフをアニメーションにしたものが以下
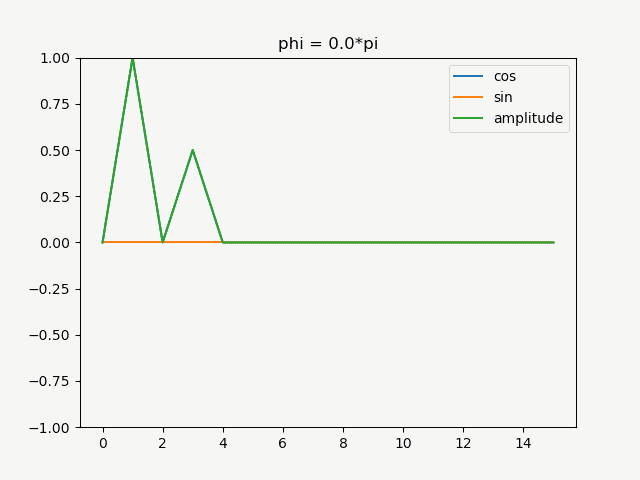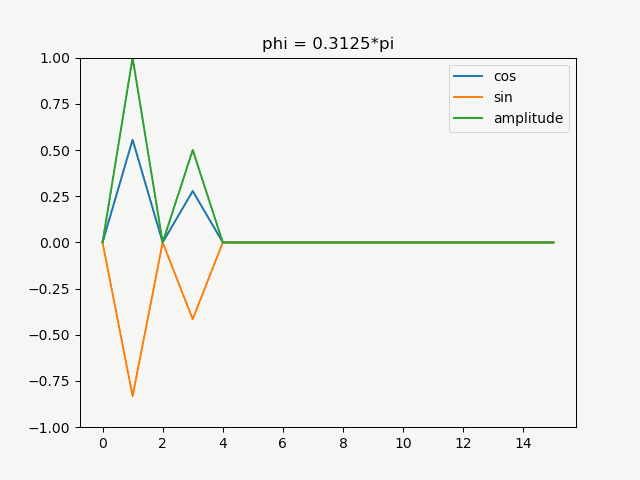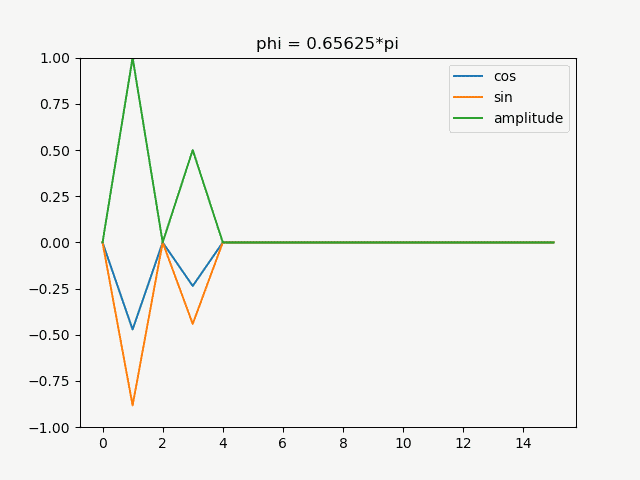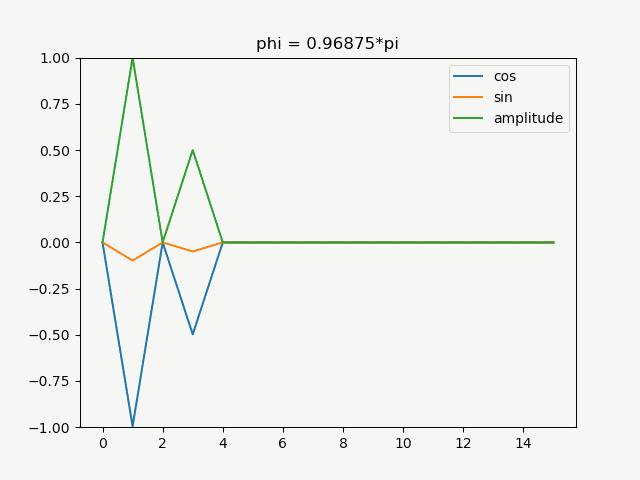
周期1と3にピークがあり、絶対値を取ったamplitudeの値は位相をずらしても変化しませんが、cosの位相をずらしたものはsinの成分に当たる虚部にも値を持ち始めることが分かります。
試しに\(\arctan(実部 / 虚部)\)を求めるとちゃんと位相のずれ量\(\phi \)と一致します。
なのでフーリエ変換は各周波数のパワーへの変換と言いながら実はcosとsinそれぞれの各周波数のパワーへの変換であり、値を2つ持つことになります。
1つの時間軸の関数だったものが、2つの周波数軸に変換されてしまう。じゃあ複素数で表現した方がすっきりするんじゃね?という事で複素数です。
すっきりするだけでなく、色々辻褄あうし、表現がしやすくなるし。そんなところだと思います。
まとめ
フーリエ級数展開は任意の式のcos/sinへの展開
フーリエ変換は任意の式をcos/sinのそれぞれのパワーへ変換
それをcosのパワーを実部、sinのパワーを虚部とした複素数で表現
パワーと位相のずれなんだし極座標で表現してもいいんだろうけどなぁ。オイラーの公式がかっこいいから複素数なのかなぁ。

コメント