離散フーリエ変換を心で理解すると、任意の関数はcos/sinの式により周期とその位相のずれで表現できることがわかりました。
任意の波に対して、sinとcosの波を乗じて和を取ることで各周期のパワーを得ることができます。
今度は離散コサイン変換に関しても心に刻もうと思います。
なんで位相のずれがあるのにcosだけで表現できるのか、直感的にはわかりにくいですが、そのあたりを考えてみたいと思います。
この解釈が正しいかどうかは怪しいですが、ひとまず辻褄は合うように思います。
離散コサイン変換
JPEGやMP3など世の中で死ぬほど使われてます。理解しましょ。
離散フーリエ変換には虚数が出てきます。計算が複雑になる、軸が2つになる。それが気に入らないので周期だけの表現にしたかった。そんな理由なのかなぁ。
Wikipediaによると何ぞいくつか種類があるらしいですが、最もポピュラーなDCT-IIの式は以下になります。
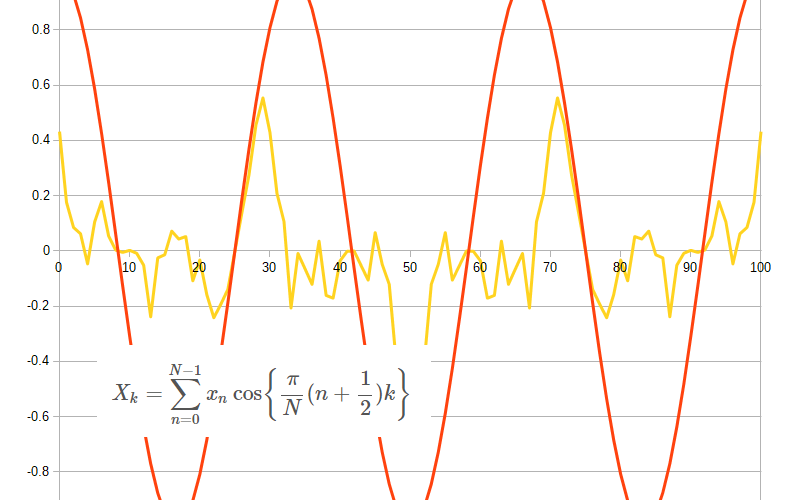
$$ X_k=\sum_{n=0}^{N-1}x_n\cos\left\{\frac{\pi}{N}(n+\frac{1}{2})k\right\} $$
式をぱっと見た感じ離散フーリエ変換の実数部だけの表現になっています。
よく見ると周期の部分が違います。離散コサイン変換はπ/N単位でシグマを取っています。離散フーリエ変換は2π/N単位です。意味としては周期を半分にして(周波数分解能を倍にして)位相のずれにあたるsinの部分を消し去っています。1/2周期位相成分をオフセットもさせています。(下で解説する折り返しの際に境界部でデータを重複させ、データ数が必ず偶数になるので中心をずらすため。なのですが細かい説明は割愛)
信号的には、信号を端っこで反転させた新たな信号に対して離散フーリエ変換を行った事と同じです。
なんで端っこで折り返すだけでsinの成分が消え去るのか?色々なWebサイトでは奇関数だからとかそんな説明がされています。グラフにしてみます。
まずは適当な乱数でグラフを書いてみます。
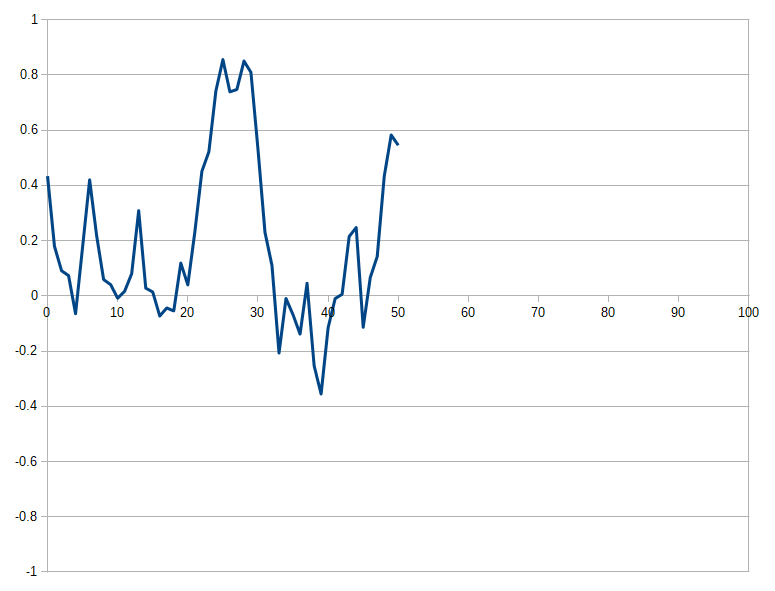
これを折り返します。
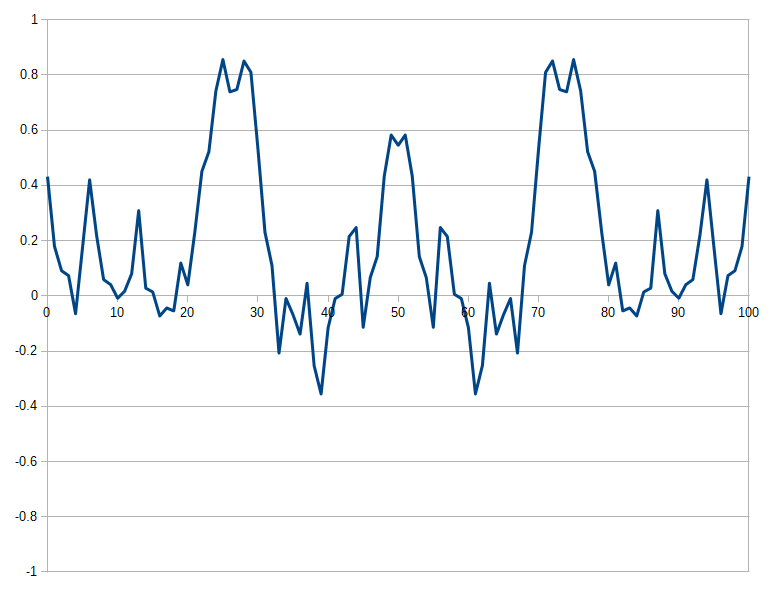
無駄にデータ数が倍になってます。このデータに対して離散フーリエ変換を行うことをイメージします。sinの成分を乗じます。
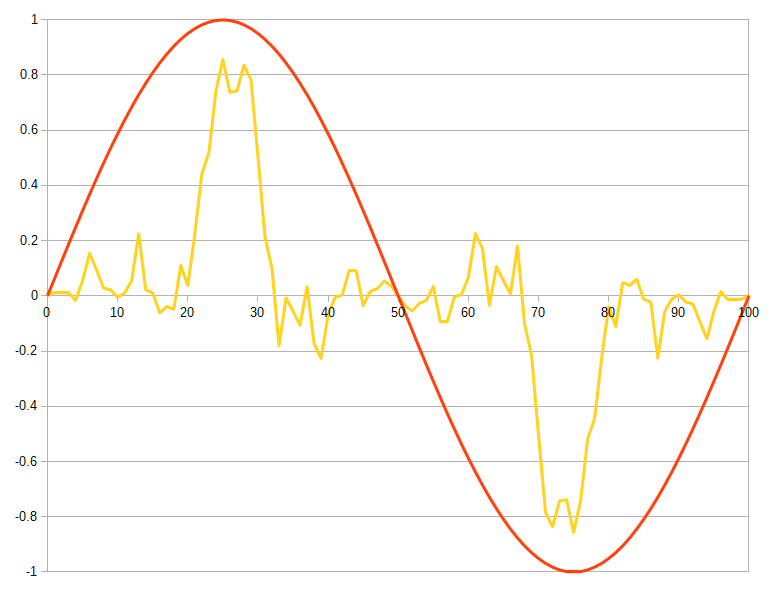
黄色いグラフが先の青い波にオレンジのsin成分を乗じた結果です。折返った部分(x = 50)でsinが負の成分を持つので打ち消しあいます。積分結果(面積)はゼロです。
もちろん周期を変えても同じです。
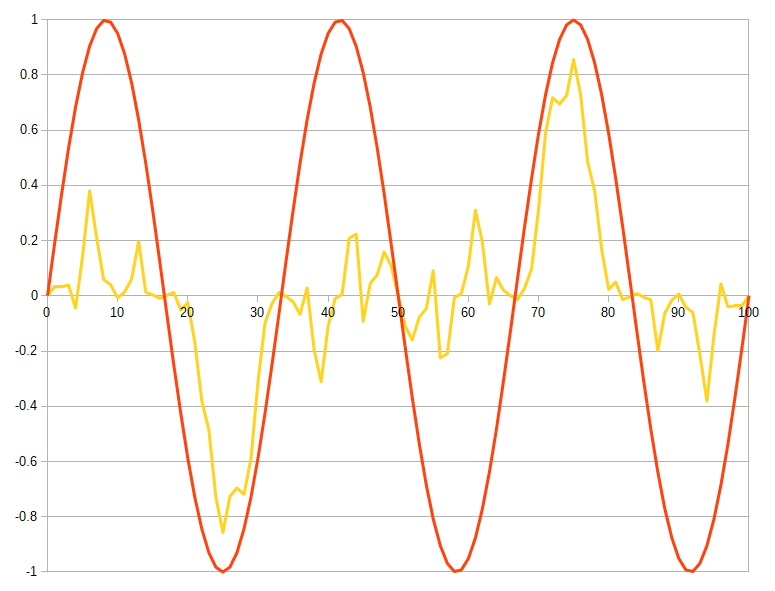
33~50の間の結果(黄色い波)は50~66の間の波が反転しており、合計を取ると打ち消しあいます。
このように折り返して描画した波に対してsinの波を乗じると、どんな周期の波でも必ず面積はゼロ。sinの成分は消え去ります。
cosに関してもやってみます。
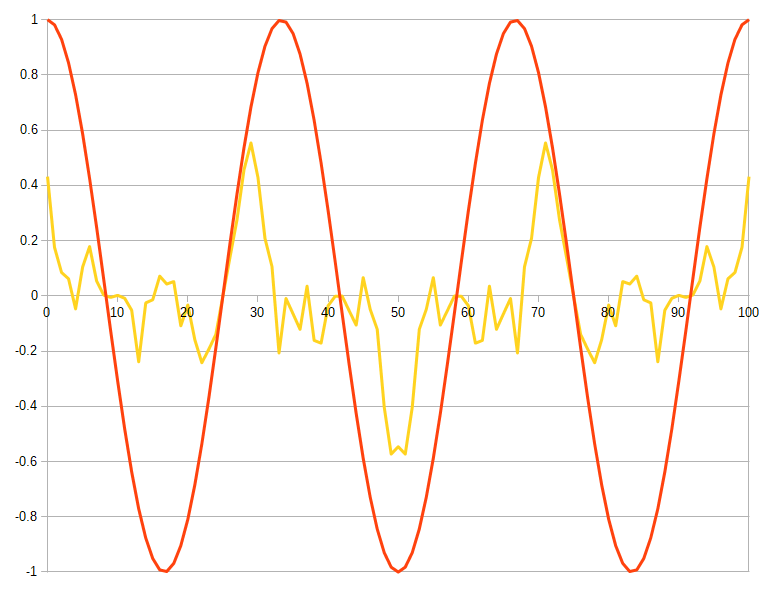
消えません。ちゃんと面積が出て成分を持ちます。(負の面積の場合もあるかもしれませんが。)
ここからなんとなくcosだけで表せる事がわかってきます。無理やり偶関数にして離散フーリエ変換のcosだけで表現したものが離散コサイン変換だ。というのが直感的な理解です。
ただ無理やり折り返してデータ数を倍にして偶関数にしたので、最大波長が倍(最小周期が半分)になったので、周波数の分解能が倍になっています。このあたりがシグマを取る時の周期が離散フーリエ変換の半分になっている訳ですな。
sinが消えて周波数分解能が倍なのでデータ量としてはとんとんですね。
まとめ
すこし不真面目に離散コサイン変換を解説しました。厳密性は勘弁してください。
同一周期の波同士の積の和でその周期のパワーがわかる。という離散フーリエ変換の時に確認した内容をベースに、sin成分を見事消し去っています。ホンマにこれで元の信号に戻るのか?というのが気になりますが、戻るんでしょうね。
計算が簡単になるらしいこの変換は広く使われている技なのでとりあえず雰囲気は理解しておくことにしましょう。


コメント