2次元デジタルフィルタを作って画像に畳みこむことで、その画像が持つ周波数を強めたり、弱めたりすることができます。いわゆるFIRフィルタとか呼ばれている基本の画像処理です。
デジタルフィルタをうまいこと作ることで特定の周波数を狙い撃ちして強めたり、なくしたりすることも原理上可能です。
原理上できるだろうなぁと思っているのですが、その実践をしてみようと思います。
1次元デジタルローパスフィルタ
まずは焦らず1次元のローパスフィルタから考えます。
ローをパスします。低い周期を通します。逆に言うとハイをカットします。特定の周波数より高い波を消し去るフィルタになります。
原理的にはある特定の波をFFTし周波数空間に持って行き、ある周波数fより高い波を0に落として、iFFTすれば良い事になります。これと同じことを実空間で実施します。
これはfより大きい値は0にし、それ以外はそのまま残す処理です。
言い換えるとこの処理は、f以下には1をそれより大きい物には0を乗じる演算になります。
周波数空間で掛け算をするとは実空間で畳み込みをすることになります。
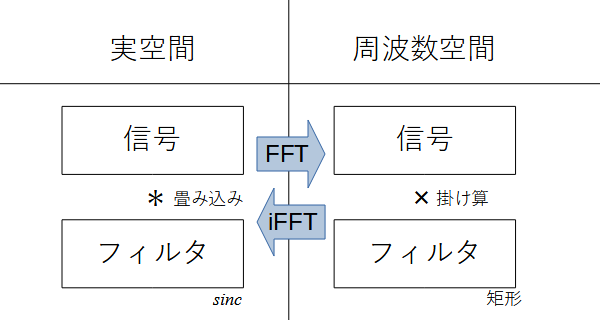
なのでこのf以下は1それ以上は0という関数をiFFTしたフィルタをオリジナルの信号に畳み込めばローパス処理の出来上がりです。
この時のフィルタがローパスフィルタになります。
矩形波の逆フーリエ変換
ある値以下の時に1でそれより大きい時は0という関数はいわゆる矩形波というやつです。方形波とも言います。パルスとも言います。多分同じです。
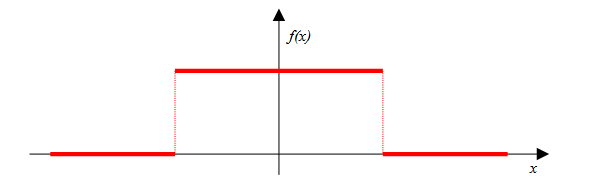
こいつのフーリエ変換結果はsinc関数になることが知られています。sinc関数は
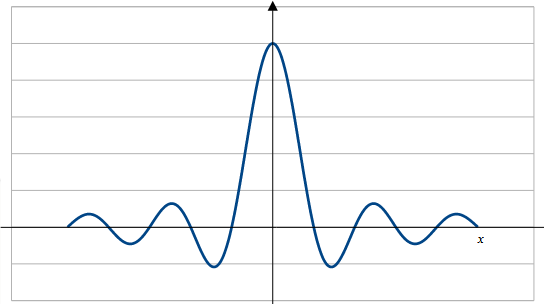
こんな関数。証明は省きます。調べると小難しい式がいっぱい出てくるサイトがいっぱい引っかかると思います。sinc関数のフーリエ変換結果は矩形波です。なのでsinc関数をオリジナルの信号に畳みこむ事でフィルタによるローパス処理ができます。
矩形波の逆フーリエ変換の畳み込み
回りくどい言い方ですが、何のことはないsinc関数を畳み込み(convolute)します。Pythonで確認します。
最終的に画像で考えたいので、1200dpiの画像に対して300dpiでカットオフするフィルタをイメージします。1200dpiだとナイキスト周波数は600dpiなのでFFTしたものはそこまで分解能があります。グラフも600dpiの信号まで表示しています。(1次元の信号ですがHzを使いません)
またsincの中心を1に持ってきたかったので、信号の数を奇数にしています。少しややこしいですがフィルタの形を奇数にしたかったので。コードです。
import numpy as np
import matplotlib.pyplot as plt
fftpt = 1201 # FFTの分解能
cent = fftpt // 2 # 中心
x = np.linspace(-300, 300, fftpt)
xx = np.linspace(-cent, cent, fftpt) # グラフの軸用
sc = np.sinc(x) # 正規化したsinc関数
sm = np.sum(sc)
sc = sc / sm # sincの積分値を1へ正規化
# 高速フーリエ変換
F = np.fft.fft(sc)
F = np.fft.fftshift(F)
plt.plot(xx,np.abs(F))
結果sincのFFT結果は、端部にひげが出てますが、ちゃんと矩形になっています。
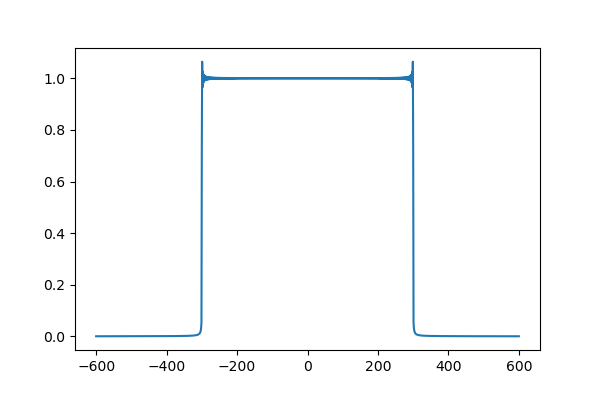
ホワイトノイズに対してsincを畳みこんで、その変換後のノイズをFFTしてみます。追加コード。今回同じ乱数を再現させたいので、seedを設定しています。
import numpy as np
import matplotlib.pyplot as plt
fftpt = 1201 # FFTの分解能
cent = fftpt // 2 # 中心
tap = 600 # フィルタのタップ数
x = np.linspace(-300, 300, fftpt)
xx = np.linspace(-cent, cent, fftpt) # グラフの軸用
sc = np.sinc(x) # 正規化したsinc関数
sm = np.sum(sc)
sc = sc / sm # sincの積分値を1へ正規化
# 高速フーリエ変換
F = np.fft.fft(zero)
F = np.fft.fftshift(F)
flt = sc[cent-tap:cent+tap+1] # フィルタの切り出し
np.random.seed(seed=1) # 乱数の再現性を出すため
noise = np.random.rand(fftpt) - 0.5 # -0.5 ~ 0.5までのホワイトノイズ
Fnoise = np.fft.fft(noise) # ノイズをFFT
Fnoise = np.fft.fftshift(Fnoise)
plt.ylim(0,30)
plt.plot(xx,np.abs(Fnoise))
smooth = np.convolve(noise, flt) # sincを畳み込み
smooth = smooth[tap:-tap]
Fsmooth = np.fft.fft(smooth) # 畳みこんだものをFFT
Fsmooth = np.fft.fftshift(Fsmooth)
plt.plot(xx,np.abs(Fsmooth))

青いグラフが元の信号。オレンジがフィルタ後の信号。きれいに重なりすぎてわかりにくいですが、周波数全域にわたってパワーを持っている元のノイズに対して、見事に300dpiより高いものがいなくなっています。
ただしこのフィルタですが、サイズ(タップ数)がバカでかいです。これでは現実的な処理になりません。フィルタの重みも遠くほど小さいのでどこかで打ち切ってやりましょう。
試しにタップ数を10で打ち切ってみます(フィルタサイズ21)。同じノイズに対して畳みこんでみます。
tap = 10 # フィルタのタップ数
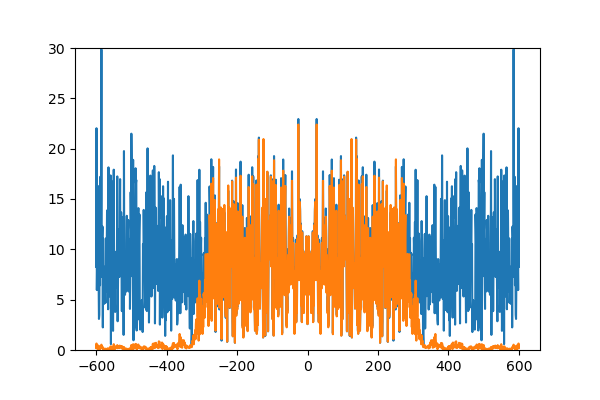
カットオフしたはずの高周波にうねり(リップル)が出ています。また低周波域も若干減衰してしまっています。
このように何も考えずに適当なサイズで打ち切ると、まぁうまく行きません。打ち切ったフィルタをFFTしてみます。
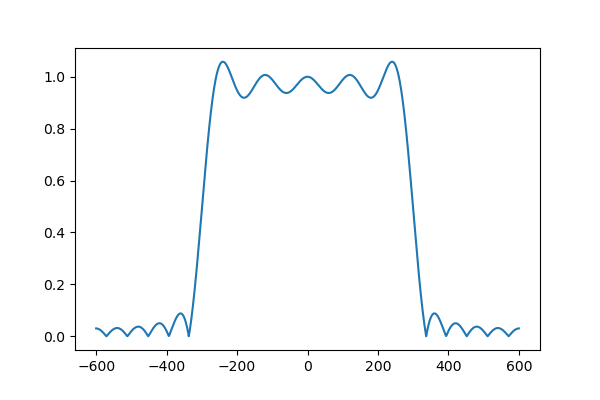
閾値となる周波数できれいに落ちてくれません。元のきれいな矩形とはだいぶ異なります。これをなくす工夫を考えます。
窓関数
このノウハウがいわゆる窓関数をかけるという操作になります。ハン窓とかハミングの窓とか色々な窓関数が世の中にはあります。周波数分解能とリップルとの間にはトレードオフが出てきます。何を重視するかで窓関数を使い分けるのだそうです。
詳細はいったん置いといて。基本のハン窓を使ってフィルタを切り出してみます。
ハン窓はこんな形。
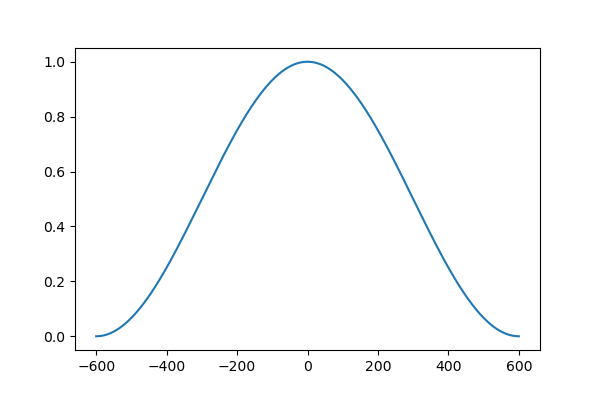
式を見ればわかりますが、何のことはないcos1周期の波です。打ち切るときに矩形ではなくcosで打ち切るという事です。フィルタの端部がきれいに減衰して周波数空間でもエッジがなまります。結果としてうねりが抑制されます。
試します。さすがpythonハン窓(ハニングの窓)1行で終わりです。
import numpy as np
import matplotlib.pyplot as plt
fftpt = 1201 # FFTの分解能
cent = fftpt // 2 # 中心
tap = 10 # フィルタのタップ数
x = np.linspace(-300, 300, fftpt)
xx = np.linspace(-cent, cent, fftpt) # グラフの軸用
sc = np.sinc(x) # 正規化したsinc関数
han = np.hanning(tap*2+1) # フィルタサイズのハン窓
hanzero = np.zeros_like(sc)
hanzero[cent-tap:cent+tap+1] = han
zero = np.zeros_like(sc)
zero[cent-tap:cent+tap+1] = sc[cent-tap:cent+tap+1]
zero = zero * hanzero # ハン窓で切り出し
sm = np.sum(zero)
zero = zero / sm # sincの積分値を1へ正規化
# 高速フーリエ変換
F = np.fft.fft(zero)
F = np.fft.fftshift(F)
flt = zero[cent-tap:cent+tap+1]
np.random.seed(seed=1) # 乱数の再現性を出すため
noise = np.random.rand(fftpt) - 0.5 # -0.5 ~ 0.5までのホワイトノイズ
Fnoise = np.fft.fft(noise) # ノイズをFFT
Fnoise = np.fft.fftshift(Fnoise)
plt.ylim(0,30)
plt.plot(xx,np.abs(Fnoise))
smooth = np.convolve(noise, flt) # sincを畳み込み
smooth = smooth[tap:-tap]
Fsmooth = np.fft.fft(smooth) # 畳みこんだものをFFT
Fsmooth = np.fft.fftshift(Fsmooth)
plt.plot(xx,np.abs(Fsmooth))
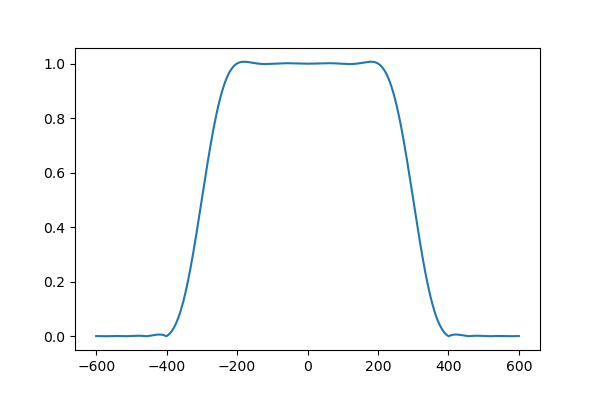
特定のサイズで打ち切ったフィルタにはあったあのうねった周波数応答が見事になまりました。
同じようにノイズに対して畳みこんでみます。
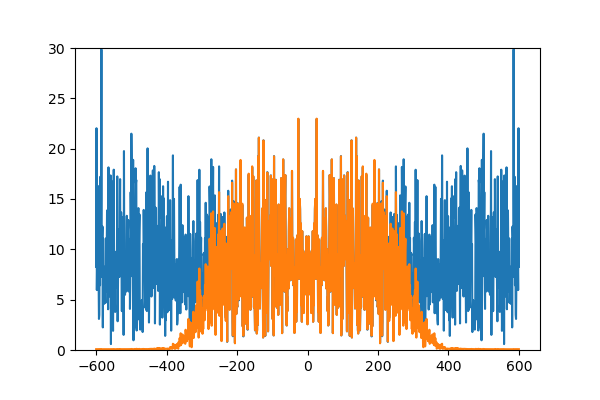
きれいです。高周波部のうねりもなくなり、また低周波部のパワーも完全に保存されています。もちろんなましているので、きれいにストンとある周期でカットされずに幅を持って減衰するようにはなってしまいますが、窓をかけないよりは全然ましです。
まとめ
とりあえず1次元の波に対してデジタルフィルタを作ってその周波数応答から、
sinc関数を畳みこむことで特定の周波数より高い波をカットできること。
sinc関数の切り出しに矩形を使うと周波数応答がうねること。
sinc関数の切り出しにハン窓を使うときれいな周波数応答をすること。
が確認できました。適当なホワイトノイズでその効果もそれなりに確認できました。次は2次元に拡張させます。


コメント