画像に対してデジタルフィルタをかける 2

　先に１次元のローパスフィルタについて簡単にまとめてみました。

　特定の周波数より高い波を捨て、低い波は極力残すようなフィルタを、sinc関数に対してハン窓を使って切り出すことで実現させました。

　任意の波に対してそのローパス効果も確認できました。今度はこれを２次元に拡張してみます。やっと画像処理っぽくなります。

2次元sinc関数
円柱関数
2次元窓関数
実験
まとめ

2次元sinc関数

　ローをパスします。低い周期を通します。１次元ではわかりやすく矩形波の逆フーリエ変換にあたるsinc関数を畳みこめばよかったのですが、２次元になるとちょっと様子が違います。結論から言うと何も考えずに2次元にしただけではうまくい来ませんでした。

　とりあえず２次元のsinc関数を考えてみます。原点からの距離に応じて波が進むようなsinc関数を作って見ます。

　これを逆フーリエ変換してプロットすると…

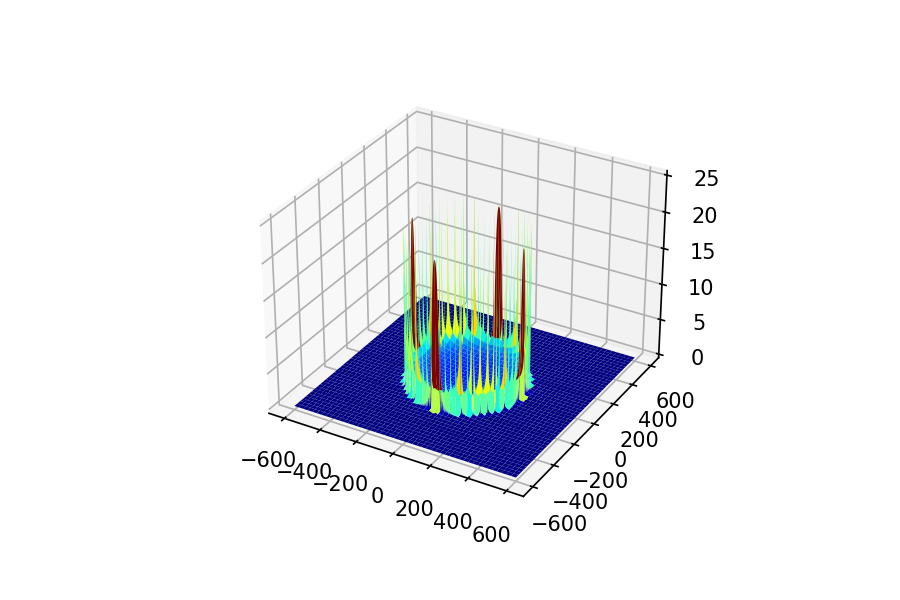
　どうもきれいな矩形波になってくれません。期待したのは円柱のような形ですが、だいぶ様子が違います。中央位置で輪切りにするとこんなグラフ。

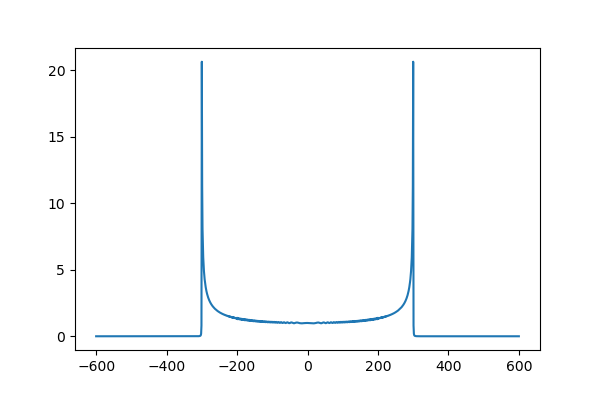
　がっかりです。ほど遠い感じ。

　2次元sinc関数の正しい作り方はx軸のsinc関数とy軸のsinc関数の積の様です。

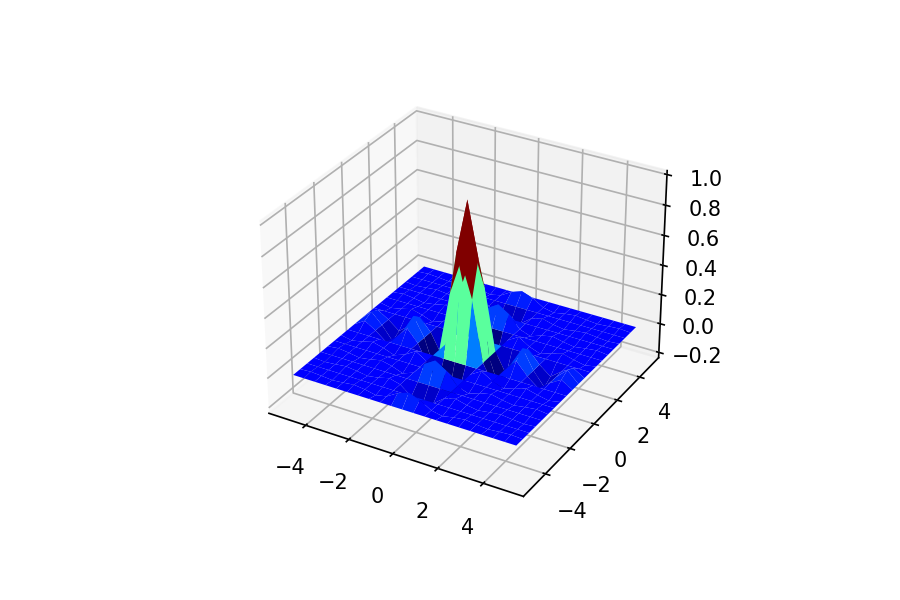
　だいぶ形がダサいですが、こいつをフーリエ変換すると

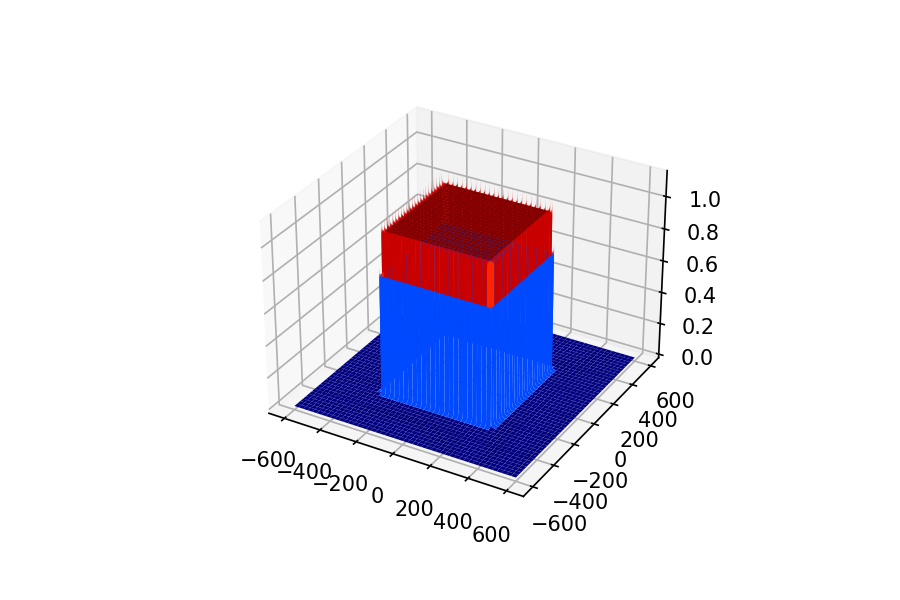
　きれいな四角い柱が出来上がりました。x方向の波、y方向の波それぞれに対してはきれいにローパスしてくれそうですが、斜め方向にはルート2倍の長さになってしまいます。期待していた応答と異なります。

円柱関数

　どうやら狙いの円柱になってくれそうな関数はsinc関数ではなく、ベッセル関数というやつだそうです。

　何やら急に数式が難解になってきましたが、さすがはpython（といかscipy）しっかり関数が用意されています。が、なんかフーリエ変換してもうまく円柱になってくれません。惜しくもない。

　色々あがいたのですが、どうにもならなかったので、あきらめました。力技に出ます。

　円柱を逆フーリエ変換してフィルタを作ります。

fftpt = 1201  # FFTの分解能

x = np.linspace(-600, 600, fftpt)

aa, bb = np.meshgrid(x,x)
grid = np.sqrt(aa**2 +  bb**2)

# 円柱関数作成
grid[grid < 300] = 1
grid[grid >= 300] = 0

# 逆FFT
f = np.fft.ifft2(np.fft.fftshift(grid))
sc = np.fft.fftshift(f).real

　円柱は適当に原点からの距離がある値以上であれば１、そうでなければ0という狙った周波数応答通りに作り、それを逆フーリエ変換してみます。すると、

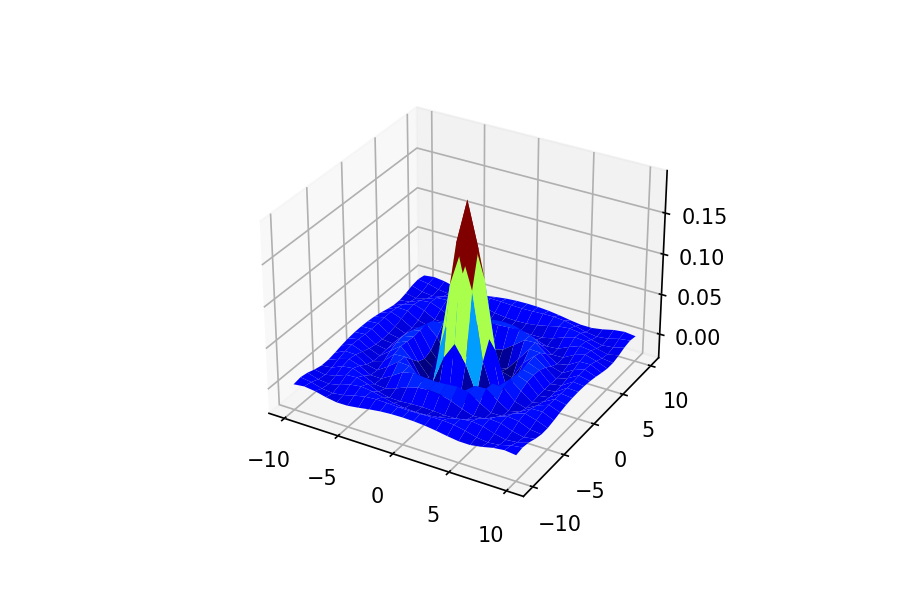
　なんかsinc関数に似てんじゃん。

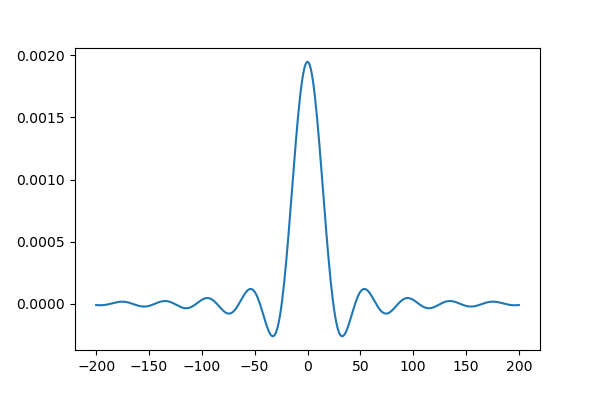
　でもちょっと違う。これをフーリエ変換して見るときちんと円柱に戻りました。

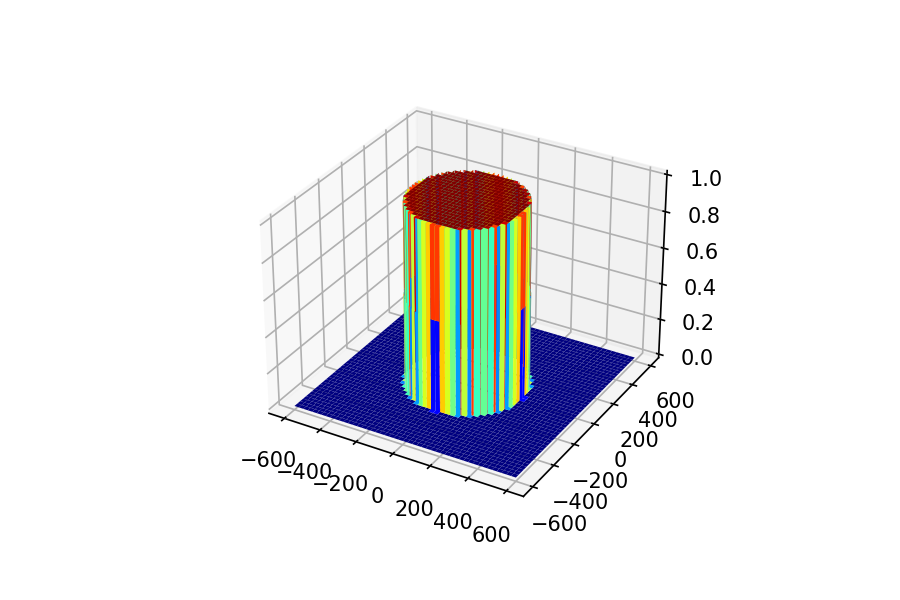
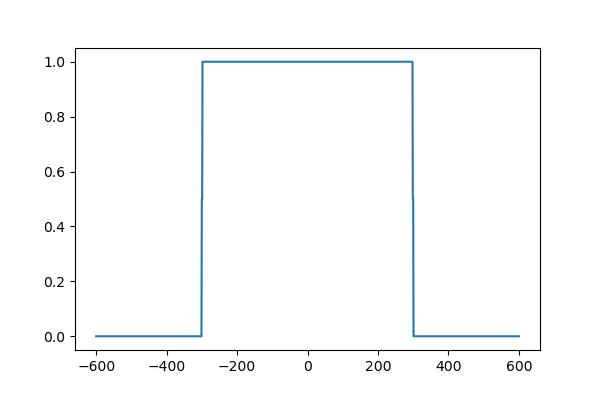
　輪切りにしてもきれいな矩形。フーリエ変換すると円柱になる配列は作り出せました。（とはいえよく見ると中心で形がきれいに折り返ってないんですよねぇ…。奇数要素で逆FFTしてるからかな…。）

2次元窓関数

　次に1次元で行ったのと同じように2次元でフィルタサイズを有限サイズに打ち切るための窓関数について考えます。

　ハン窓を2次元に拡張するだけです。とはいえこの2次元ハン窓（2次元ハニングの窓）ですがpythonに関数がなさそうです。ほんとかな。見つからなかったです。なので自作します。中心からの距離を引数にcosするだけなので簡単です。

###
# sizeは窓の1辺の長さ。奇数
def han2d(size):
    tap = size // 2    
    rad = np.linspace(-np.pi, np.pi, 2*tap+1) # -pi ~ pi
    radx, rady = np.meshgrid(rad, rad)
    radgrid = np.sqrt(radx**2 + rady**2) # 原点からの距離を示したグリッド
    radgrid[radgrid > np.pi] = np.pi # piより大きいものはpiにクリップ（四隅）
    han2 = 0.5 + 0.5 * np.cos(radgrid) # ハン窓の定義
    return han2

　こんな感じです。

　追記：任意の2次元窓関数をもっと簡便に作る方法を考えました。

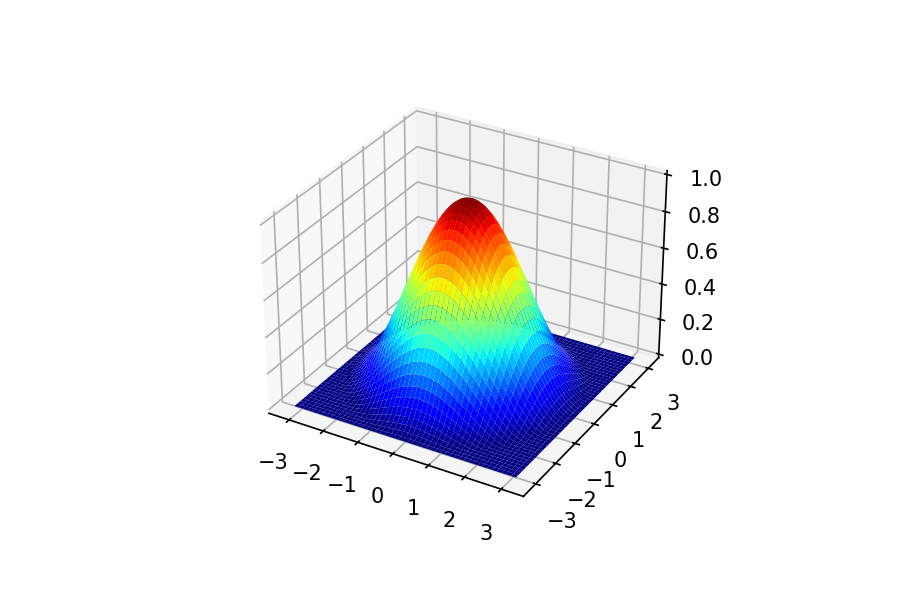
　この窓関数を掛けてフィルタを現実的なサイズに打ち切ります。

　そして得られた21×21フィルタの周波数応答がこれ

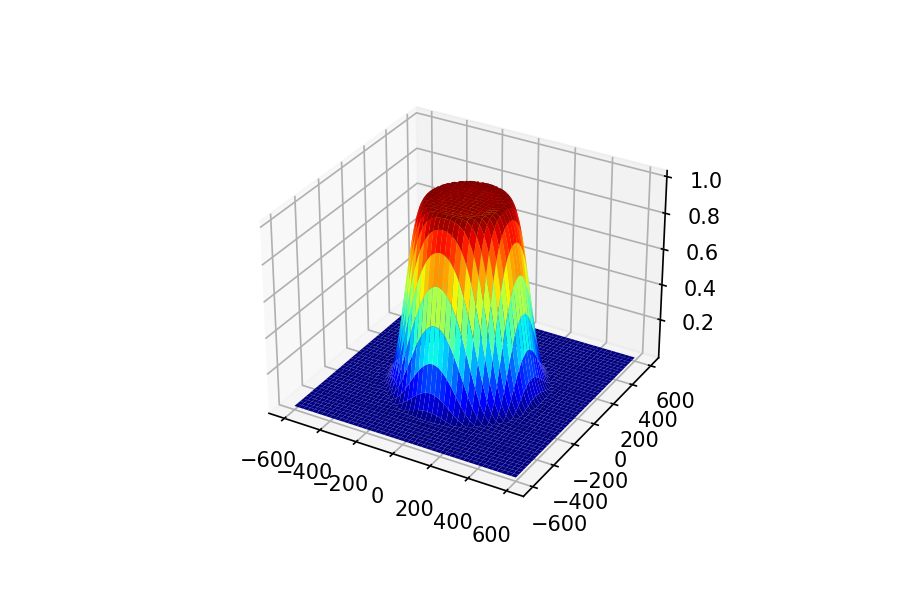
　円柱がプリンみたいになりましたが狙い通りです。試しに窓関数を掛けずに21×21に打ち切ると

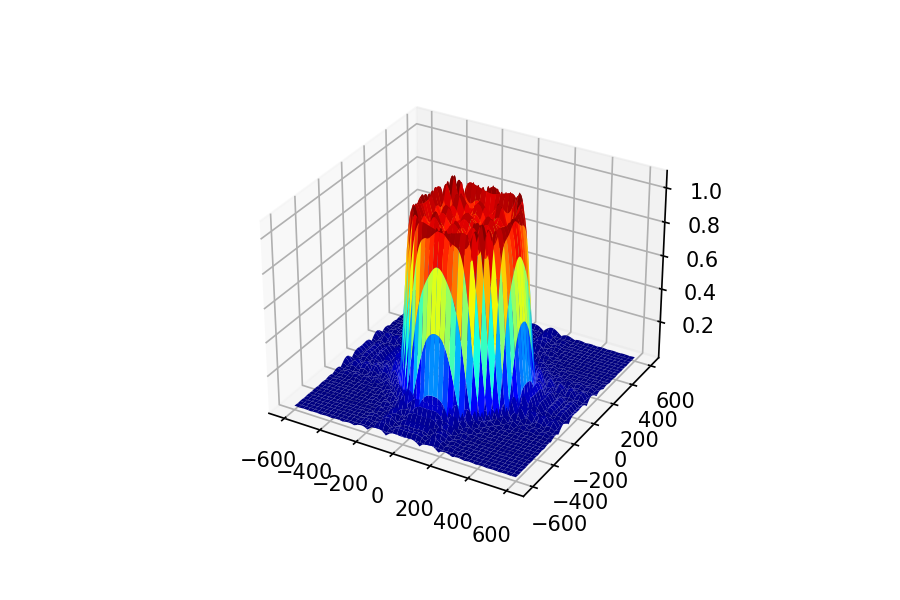
　1次元の時と同じような感じですね。がったがたです。2次元でも窓の効果アリです。フィルタの完成です。

実験

　色々な周期を持った2次元の画像に対してこのフィルタを畳みこんでみます。

　狙った周波数以上の波だけ減衰し、それ以下が残っていればひとまず思惑通りということになります。まずはそのターゲットとなる色々な周期を持った画像を作るところからです。

　適当な周期のcos波を発生させてそれを２次元に広げて画像化してみます。同心円を作るイメージです。画像の中央からの距離をそのままcosの引数にして、その振幅を画像化してみます。コードにするとこんな感じ。

###
# ２次元の同心円画像を発生
def imggen():
    x = np.linspace(-20*np.pi, 20*np.pi, 2048) # 画像サイズは2048x2048
    xx,yy = np.meshgrid(x, x)
    dis = (xx**2 + yy**2) / 4
    cos = (0.5*np.cos(dis) + 0.5) * 255
    
    return cos.astype(np.uint8)

　まぁもっともらしい感じの画像になりました。縮小して見ると完全にモアレが出てしまっています。（ピクセル等倍の画像で置いておきます。）この画像に対して作成したフィルタを畳みこんでみます。先のフィルタを使って、この画像に対してopencvのfilter2D関数で畳みこんでみます。

　コードです。

fftpt = 1201  # FFTの分解能
cent = fftpt // 2  # 中心
tap = 10 # フィルタのタップ数

x = np.linspace(-600, 600, fftpt)
xx = np.linspace(-cent, cent, fftpt)

aa, bb = np.meshgrid(x,x)
grid = np.sqrt(aa**2 +  bb**2)

# 円柱関数作成(カットオフ周波数 300dpi)
grid[grid < 300] = 1
grid[grid >= 300] = 0

# 逆FFT
f = np.fft.ifft2(np.fft.fftshift(grid))
sc = np.fft.fftshift(f).real

# ハン窓を掛けた切り出し
han = han2d(tap*2+1)
hanzero = np.zeros_like(sc)
hanzero[cent-tap:cent+tap+1, cent-tap:cent+tap+1] = han
zero = sc * hanzero

# 正規化
sm = np.sum(zero)
zero = zero / sm

img = imggen() # 同心円画像の発生

# 21x21 フィルタの切り出し
flt = zero[cent-tap:cent+tap+1, cent-tap:cent+tap+1]
out = cv2.filter2D(img, -1, flt) # 畳み込み
cv2.imwrite("testout.png", out)

　入力画像のナイキスト周波数のさらに半分を減衰させるようなフィルタを作っているので、4画素周期の波までは減衰しそれより低い波は残る。はずです。（1200dpiの画像（600dpiまで解像できる）に対して300dpiでカットオフしているつもり。）

　結果としてはまぁそんな感じに見えなくもない。試しにさらに半分の周波数までカットオフしたものと並べてみます。