360度カメラで撮影した写真を任意の視点からの画像（パノラマ画像）へ変換するビューアーを作ってみようと思います。その最終回です。
1.360度写真の平面投影
2.視点の変更と背面の投影
3.視点の回転
前回までの記事でひとまず適当な全天球画像からそれっぽい画像へ変換することはできました。
今回はその続きです。画像をグルグルまわして、好きな角度の画像を切り出してみようと思います。
回転
前回までの記事で全天球画像専用のビューアーで見るような画像へ変換することができました。ただ現状はとある一視点だけです。専用ビューアーのように画像をグルグルまわしてみます。
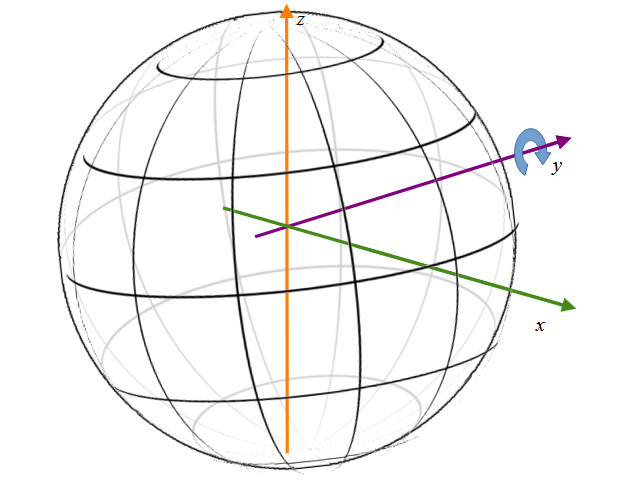
視点のイメージはコレ。球体に張り付けた全天球画像を球の中から観察するイメージです。
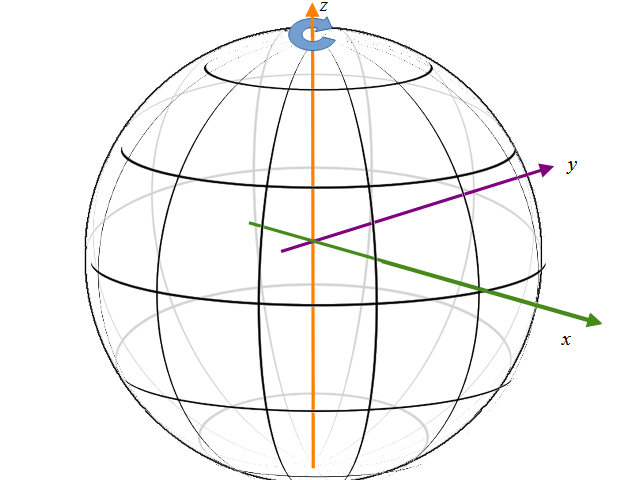
画像をグルグルまわします。これを視点の位置を変えるのではなく、球上のxyzの座標をまわすことで代替します。
視点を変えるのではなく、球に張り付いた画像の方をまわすイメージになります。視点は固定で周りの風景がグルグル回ることになります。
3次元座標の回転
得られる2次元の画像座標が３次元のどこの座標から投影されているかは、前回までの記事のように比較的簡単に計算できます。
視点と投影面の関係は
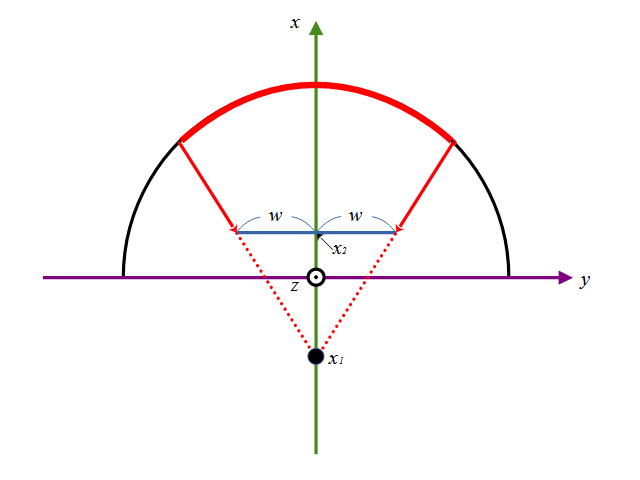
このように定義します。視点をx軸上のとある座標\(x_1\)とし、撮像面の座標を\(x_2\)とします。そこに幅2wの面をおいて、そこに投影される球面の座標をxyzとします。この座標を回転させてみます。３次元なのでx,y,z軸それぞれに対して回転が定義できます。
例えばy軸を回転軸として回転を考えてみます。図にするとこんな感じになります。
視点とその向きはそのままに、球の方をこんなして回転させたときに得られる画像としては、首を上下に振ったようなものになります。
上を見上げたり、下を見下げたり。
xz平面で考えると単純な２次元の回転のアフィン変換です。y軸を回転軸にしているのでyの値は回転前後で変化しません。
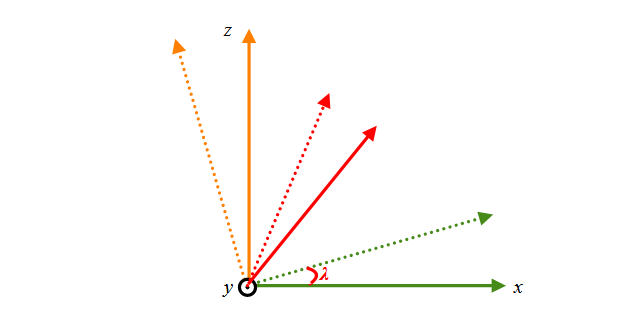
もっともらしい式で表現するとこんな感じになります。回転軸にあたるｙの成分は変化せず、ｘとｚの値がλだけ回転しています。
$$ \left(\begin{array}{c}\cos\lambda & 0 & \sin\lambda \\ 0 & 1 & 0 \\ -\sin\lambda & 0 & \cos\lambda\end{array}\right) \left(\begin{array}{c}x\\ y \\ z\end{array}\right) $$
同じようにx軸を回転軸にするとこんな感じ。首を横に傾げたイメージ。
同様に式は
$$ \left(\begin{array}{c}1 & 0 & 0 \\ 0 & \cos\lambda & \sin\lambda \\ 0 & -\sin\lambda & \cos\lambda\end{array}\right) \left(\begin{array}{c}x \\ y \\ z\end{array}\right) $$
z軸を回転軸にするとこんなイメージ。首を横に振ったイメージ。
式
$$ \left(\begin{array}{c}\cos\lambda & \sin\lambda & 0 \\ -\sin\lambda & \cos\lambda & 0 \\ 0 & 0 & 1 \end{array}\right) \left(\begin{array}{c}x\\ y \\ z\end{array}\right) $$
この３つの回転行列を順番に掛け算することで任意の回転補正が可能になります。
お手本にしているTHETAのビューアーだとx軸の回転はサポートされていないようです。カメラの水平は保たれていることを前提にしているようです。（もしくはジャイロセンサで取って勝手に補正しているのかも。）
ロール・ピッチ・ヨー
何ぞ呪文のようですが、一般的に回転軸はロール・ピッチ・ヨーの名前で呼ばれているようです。カメラの手振れ補正装置、ジンバルでもそんな感じで呼ばれるのが一般的のようです。
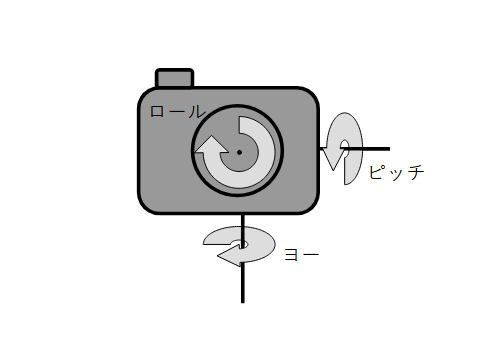
今回の回転軸で考えると、x軸がロール、y軸がピッチ、z軸がヨーになります。カメラの世界で使われているそれと同じ軸です。
Pythonで記述
Pythonで記述してみます。詳細は過去の2記事を参考にしてもらえるとわかると思います。
import numpy as np
import cv2
img_w = 1920
img_h = 1080
senser_w = 0.75
senser_h = 0.75 * img_h / img_w
x1 = -1.2 # 視点の位置
x2 = 0.5 + x1 # 撮像面の位置(必ず視点より前)
# 回転量
roll = 45.0 * np.pi / 180
pitch = 45.0 * np.pi / 180
yaw = 45.0 * np.pi / 180
# 3次元の回転行列
mtx1 = np.array([[1, 0, 0],
[0, np.cos(roll), np.sin(roll)],
[0, -np.sin(roll), np.cos(roll)]])
mtx2 = np.array([[np.cos(pitch), 0, -np.sin(pitch)],
[0, 1, 0],
[np.sin(pitch), 0, np.cos(pitch)]])
mtx3 = np.array([[np.cos(yaw), np.sin(yaw), 0],
[-np.sin(yaw), np.cos(yaw), 0],
[0, 0, 1]])
# 回転行列の積
mtx4 = np.dot(mtx3, np.dot(mtx2, mtx1))
w = np.arange(-senser_w, senser_w, senser_w * 2 / img_w)
h = np.arange(-senser_h, senser_h, senser_h * 2 / img_h)
# センサの座標
ww, hh = np.meshgrid(w, h)
# 直線の式
a1 = ww / (x2 - x1)
a2 = hh / (x2 - x1)
b1 = -a1 * x1
b2 = -a2 * x1
a = 1 + a1**2 + a2**2
b = 2 * (a1 * b1 + a2 * b2)
c = b1**2 + b2**2 - 1
d = (b**2 - 4*a*c) ** (1/2)
# 球面上の3次元座標
x = (-b + d) / (2 * a)
y = a1 * x + b1
z = a2 * x + b2
# 座標の行列計算
xd = mtx4[0][0] * x + mtx4[0][1] * y + mtx4[0][2] * z
yd = mtx4[1][0] * x + mtx4[1][1] * y + mtx4[1][2] * z
zd = mtx4[2][0] * x + mtx4[2][1] * y + mtx4[2][2] * z
# 緯度・経度へ変換
phi = np.arcsin(zd)
theta = np.arcsin(yd / np.cos(phi))
xd[xd > 0] = 0
xd[xd < 0] = 1
yd[yd > 0] = np.pi
yd[yd < 0] = -np.pi
ofst = yd * xd
gain = -2 * xd + 1
theta = gain * theta + ofst
img = cv2.imread("src.jpg")
img_h, img_w = img.shape[:2]
# 画像座標へ正規化
phi = (phi * img_h / np.pi + img_h / 2).astype(np.float32)
theta = (theta * img_w / (2 * np.pi) + img_w / 2).astype(np.float32)
out = cv2.remap(img, theta, phi, cv2.INTER_CUBIC)
cv2.imwrite("dst.jpg", out)
だいぶ長くなってきましたが、前回までのコードに対して、回転行列の演算が追加されただけです。なので今回のポイントは
# 回転量
roll = 45.0 * np.pi / 180
pitch = 45.0 * np.pi / 180
yaw = 45.0 * np.pi / 180
# 3次元の回転行列
mtx1 = np.array([[1, 0, 0],
[0, np.cos(roll), np.sin(roll)],
[0, -np.sin(roll), np.cos(roll)]])
mtx2 = np.array([[np.cos(pitch), 0, -np.sin(pitch)],
[0, 1, 0],
[np.sin(pitch), 0, np.cos(pitch)]])
mtx3 = np.array([[np.cos(yaw), np.sin(yaw), 0],
[-np.sin(yaw), np.cos(yaw), 0],
[0, 0, 1]])
# 回転行列の積
mtx4 = np.dot(mtx3, np.dot(mtx2, mtx1))
この部分。任意の向きへ画像をぐるっとまわすために、ヨー・ピッチ・ロールの3つの角度を持つ行列の積をとっています。上記で説明したまんまのコードです。この3×3の回転行列を得られたxyzの3次元座標に対して乗じることで、座標を球面上回転させます。この例では適当にすべて45度まわしています。この行列を
# 座標の行列計算 xd = mtx4[0][0] * x + mtx4[0][1] * y + mtx4[0][2] * z yd = mtx4[1][0] * x + mtx4[1][1] * y + mtx4[1][2] * z zd = mtx4[2][0] * x + mtx4[2][1] * y + mtx4[2][2] * z
得られた3次元座標に対して乗じ、新たな3次元座標を得ています。
結果
適当な角度でまわしてみます。3つの軸で一度にまわしてみます。
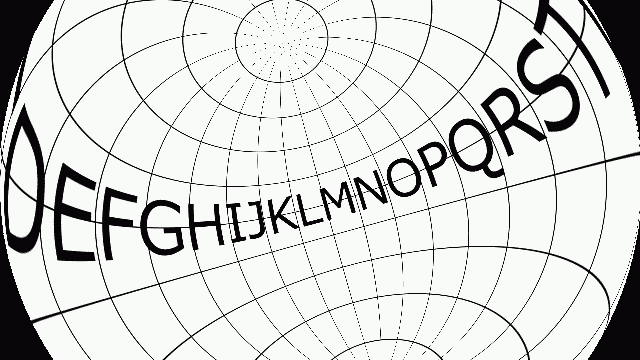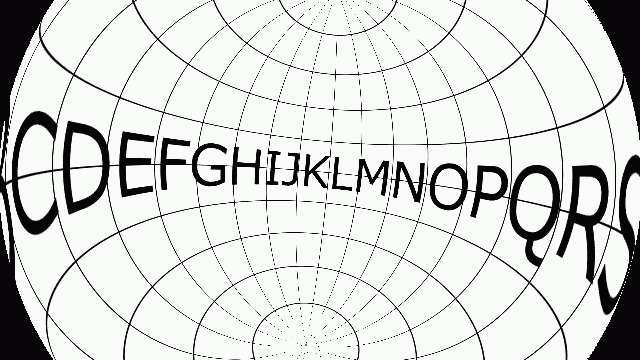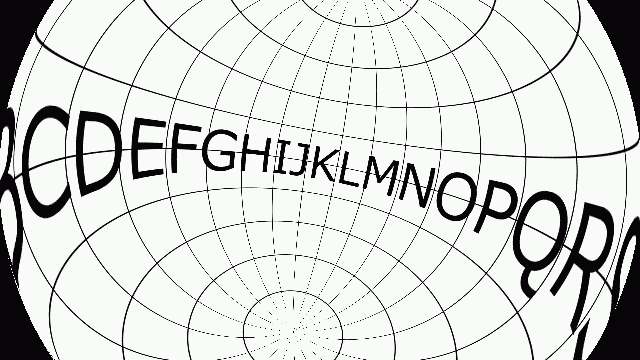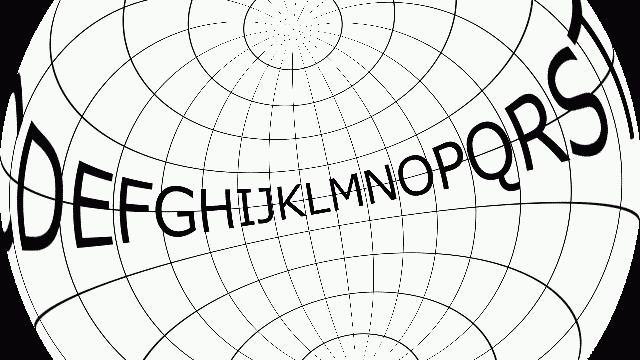
まぁ想定通りです。
実際撮影した画像でもまわしてみます。
実際にカメラを動かしてるがごとくシーンが変化しています。もっとフレームレートを上げたらもっともらしい動画になりそうです。
まとめと今後
3回かけて全天球画像から任意視点の画像を描画することができました。実際の写真で試してもそれっぽい結果が得られています。ひとまず目標としていたTHETAのビューアーライクなことはできそうです。
応用すれば、360度動画から手振れ補正もできそうです。上下左右の情報さえあればジンバルのように補正ができるはずです。
また固定の360度カメラからの被写体の追跡も面白そうです。これらの座標変換の基本ができればその応用範囲も広そうです。機会があれば試してみたいと思います。
コメント