多項式近似をPythonで行う場合に便利なpolyfit関数ですが、y切片0の近似曲線を作ってくれません。エクセルだとチェックボックスつけるだけで簡単にできてしまうこれが、Python使って気軽にできないのは悔しいので、方法を探ります。
今回は原点を通るだけでなく、任意の点を通る関数近似も作ります。3次多項式で試しますが、何次でも同じです。
y切片0の多項式近似
今回はひとまず3次の多項式で考えます。通常近似される多項式は
$$ y=ax^3 + bx^2 + cx + d $$
で示されるa~dの4つの定数を使って表現されます。この定数群を最小二乗法で見つけてくれる関数が、polyfit関数になります。1行です。ただしdも値を持ってしまいます。
y切片0、すなわち原点を通るということは、d=0になります。この制約を入れて誤差を最小化したいのですが、関数一つではできません。
scikitlearnを使うとできるらしいのですが、numpyだけでもできちゃうのでそちらの方法で攻めます。
これは行列計算使って簡単に求めることができます。理屈や詳細は別記事参照。
関数で表現すると
# 原点を通る回帰
def mypolyfit0(x, y):
X1 = np.stack([x**3, x**2, x], 1)
invX1 = np.linalg.inv(np.dot(X1.T, X1))
X1tY = np.dot(X1.T, y)
return np.append(np.dot(invX1, X1tY), 0)
こんな感じ。この関数の返り値がそのまま上の式のa,b,c,dになります。
4次であれば
X1 = np.stack([x**4, x**3, x**2, x], 1)
こうなるだけです。面倒なので変数にはしませんでしたが。
numpyでやりたければこれを使ってください。
任意の点を通る多項式近似
先の方法は原点を通る場合でしたが、例えば任意の点\((x_1,y_1)\)を通るような制約を入れるのも簡単です。この点を通る多項式なので、
$$ y_1=ax_1^3 + bx_1^2 + cx_1 + d $$
が成り立ち、dについて解くと、
$$ d=y_1 – ax_1^3 – bx_1^2 – cx_1 $$
これを元の多項式に代入して整理すると
$$ y – y_1 = a(x^3 – x_1^3) + b(x^2 – x_1^2) + c(x – x_1)$$
となり、この線形回帰をすれば良いことになります。これもPythonの関数で表現すると、
# ある点(x1,y1)を通る回帰
def mypolyfit(x, y, x1, y1):
X1 = np.stack([(x**3 - x1**3), (x**2 - x1**2), (x - x1)], 1)
invX1 = np.linalg.inv(np.dot(X1.T, X1))
X1tY = np.dot(X1.T, y - y1)
ans = np.dot(invX1, X1tY)
d = y1 - ans[0]*x1**3 - ans[1]*x1**2 - ans[2]*x1
return np.append(ans, d)
となるだけです。先の切片はこの式のx_1=0、y_1=0の時にあたります。たまに特定の点を通る回帰がしたくなります。(255,255)を通るようにとか。そんな時はこの関数で求めることができます。
原点と任意の点の2点を通る多項式近似
今度はちょっとややこしいですが、たま~に使いたくなります。例えば原点と(255,255)を通る多項式が欲しい時とか。
これももう一つ制約を入れるだけです。原点を通るのでd=0は確定しています。そのため
$$ y_1=ax_1^3 + bx_1^2 + cx_1$$
からcについて解くと
$$ c = \frac{y_1}{x_1} – ax_1^2 – bx_1 $$
これを元の式に代入して、整理すると、
$$ y – \frac{y_1}{x_1}x = a(x^3 – x_1^2 x) + b(x^2 – x_1 x)$$
となるので、この線形回帰になります。変数が2つになってしまいました。これも関数にしてみます。
# 原点ともう一点通る回帰
def mypolyfit2(x, y, x1, y1):
X1 = np.stack([(x**3 - x1**2*x), (x**2 - x1*x)], 1)
invX1 = np.linalg.inv(np.dot(X1.T, X1))
X1tY = np.dot(X1.T, y - (y1/x1)*x)
ans = np.dot(invX1, X1tY)
c = y1/x1 - ans[0]*x1**2 - ans[1]*x1
return np.append(np.append(ans, c), 0)
これで完成です。
検算
リファレンスとなるpolyfitとの比較を行い、上記の関数の妥当性を確認してみます。
コードは
x = np.linspace(0,20,201)
y = -0.005*x**3 + 0.15*x**2 + 0.001*x + 0.0
#近似式(リファレンス)
ref = np.polyfit(x,y,3)
yref = np.poly1d(ref)(x)
type1 = mypolyfit0(x,y) # 切片0
type2 = mypolyfit(x,y,20,20.02) # 20,20.02を通る曲線
type3 = mypolyfit2(x,y,20,20.02) # 原点と20,20.02を通る曲線
y1 = np.poly1d(type1)(x)
y2 = np.poly1d(type2)(x)
y3 = np.poly1d(type3)(x)
#グラフに表示
plt.plot(x,y)
plt.plot(x,yref)
plt.plot(x,y1)
plt.plot(x,y2)
plt.plot(x,y3)
plt.show()
3次の線形回帰pyfyfitは
ref = np.polyfit(x,y,3)
こんなんで表現できてしまいます。
まず適当なx,yの対を用意します。
x = np.linspace(0,20,201)
y = -0.005*x**3 + 0.15*x**2 + 0.001*x + 0.0
これはxを0~20まで200点用意して、yを適当な3次関数で作ります。原点と20.02を通る曲線になります。グラフにすると
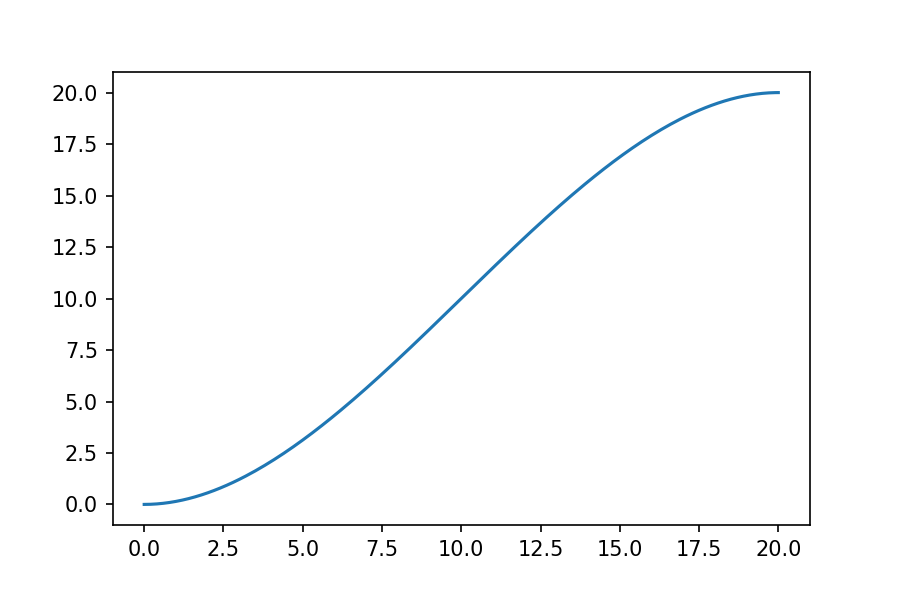
こんなカーブです。近似の結果は完全に一致します。今回実際に通る点を指定してみましたが、座標指定した近似だけ微妙に値がずれました。が実害のないレベルの誤差に見えます。
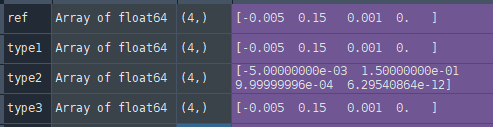
ひとまずこんなものでしょう。関数をもっと適当なものにしてみたり、乱数を加えてみたりすると面白いです。ちゃんと近似してくれるので。



コメント