最小二乗法による近似式を求めることがたまにあります。そんな時は、エクセル使ってチャチャっと求める。ただ理屈がわかっていません。もう少し突っ込んだ理解をしようと思います。
行列で記述
このあたりを丁寧に説明してくれているサイトがあった。ココです。このページも読みました。「最小二乗法の行列による定式化」に関して詳しい説明がある。が、ちんぷんかんぷんだ。何を言ってるんだ?今回の目標はここに書いてあることを理解するまで頑張る。
というわけで紙と鉛筆を使って、式をゴリゴリ解いてみる。
最小二乗法による1次直線フィッティング
行列はなじめない。というわけでまずは\(\sum\)を使って勝負する。それであれば高校数学の範囲。1次関数なので、フィッティングする式は
$$y=ax+b$$
である。この \(x\)と\(y\)がデータとして複数(\(n\)個)あるとする。このデータを上記式にフィッティングさせる。この時発生する誤差\(Err\)の二乗和を最小にするので、
$$Err=\sum_i^n(ax_{i}+b-y_{i})^{2}$$
を最小にすればよい。まだついていける。ココは泥臭く展開する。
$$Err= \sum_i^n(a^{2}x _{i} ^{2}+2abx _{i} -2ax _{i} y _{i} -2by _{i} +b^{2}+y _{i} ^{2})$$
今回は最終的に、\(a\)と \(b\) を求める問題なので、 \(a,b\)が変数で、 \(x,y\)が定数になる。 ここで\(a\)に着目すると、 \(Err\)を最小にする際に \(b\) は直接関係ない。なので、 \(b\)も\(a\)にとっては定数。
というわけで、\(a\)を変数とした式としてみると、ただの下に凸の2次関数であることがわかる。結果の最小値を求めるには、偏微分して、極値を求めればよい。
というわけで、偏微分してみる。
$$\frac{\partial}{\partial a}\sum (a^{2}x_{i} ^{2}+2abx_{i} -2ax_{i} y_{i} -2by_{i} +b^{2}+y_{i} ^{2})$$
$$=(2a\sum x^2_{i}+2b\sum x_{i}-2\sum x_{i}y_{i})$$
まだ\(\sum\)が残る。この結果が0になる時の\(a\)なので、最終的には、
$$a\sum x^2_{i}+b\sum x_{i}=\sum x_{i}y_{i}$$
となる。同様に\( b \)に関しても解くと、
$$a\sum x_{i}+b\sum 1=\sum y_{i}$$
同じような式になる。これはただの連立方程式。これなら面倒だけど解けそうな気がする。まだ高校数学の範囲。こっちの記事では連立方程式を試しました。
ただ、ここでもう1ステップ行列式への展開ができそう。というわけで、行列で表現すると、
$$\left(\begin{array}{c}\sum x_{i}^2 & \sum x_{i} \\ \sum x_{i} & \sum 1 \end{array}\right)\left(\begin{array}{c}a\\ b\end{array}\right)=\left(\begin{array}{c}\sum x_{i}y_{i}\\ \sum y_{i}\end{array}\right)$$
こんな感じ。なんかすっきりしている。ここまで来ると、このサイトで説明されている、式に近いそれができている。
\(\left(\begin{array}{c}x_{1} & 1\\ x_{2} & 1\\ : & : \\ x_{n} & 1\end{array}\right)\)を \(A\)とし、その転置は \(\left(\begin{array}{c}x_{1} & x_{2} & .. & x_{n}\\ 1 & 1 & .. & 1\end{array}\right)\) と表現され、\(A^{\top}\)となり、最後\(\left(\begin{array}{c}a\\ b\end{array}\right)\)を \(x\)とすると、左辺は、このサイトで示される\(A^{\top}Ax\)そのものになっている。
右辺に関しても、同様に \(A^{\top}\) に\(b\)=\(\left(\begin{array}{c}y_{1} \\ y_{2} \\ : \\ y_{n} \end{array}\right)\)をかけたものなので、完全に同じ式に到達している。
$$ A^{\top} Ax=A^{\top}b$$
この \(A^{\top}A\)の逆行列を求めて、右辺の左から掛けてやれば、\(x\)は求まる。
$$x=(A^{\top} A)^{-1}A^{\top}b$$
これにより近似直線をなす\(a,b\)が求められる。
最初に戻って、この式
$$Err=\sum_i^n(ax_{i}+b-y_{i})^{2}$$
は先の定義で示した式を用いて表現すると、
$$Err=(Ax-b)^{\top}(Ax-b)$$
これを\(x\)で微分すると、またもや同じ式になる。(これは行列の微分の公式を調べた)
つまり\(\sum\)を使っていろいろ回り道をしたが、最初の誤差を求める式を行列表現できさえすれば、後はその行列の微分から誤差最小となる\(x\)が求められる。と理解しました。泥臭い計算は不要だ。
最小二乗法による2次曲線フィッティング
続いては2次曲線へのフィッティング。先のページにあるように、行列で書くと、特段その表現が変わるわけではない。が、やはり今回も\(\sum\)で勝負する。
$$y=ax^2+bx+c$$
で近似する。今度は\(a,b,c\)の3変数になる。その誤差は
$$Err=\sum_i^n(ax_{i}^2+bx_{i}+c-y_{i})^{2}$$
同様に、誤差最小となるなるようなそれらを求めるために、この3変数でそれぞれ偏微分する。
$$a\sum x^4_{i}+b\sum x^3_{i} +c\sum x^2_{i} =\sum x^2_{i}y_{i}$$
$$a\sum x^3_{i}+b\sum x^2_{i} +c\sum x_{i} =\sum x_{i}y_{i}$$
$$a\sum x^2_{i}+b\sum x_{i} +c\sum 1 =\sum y_{i}$$
これを同様に行列表現すると、
$$\left(\begin{array}{c}\sum x_{i}^4 & \sum x_{i}^3 & \sum x_{i}^2 \\ \sum x_{i}^3 & \sum x_{i}^2 & \sum x_{i}\\ \sum x_{i}^2 & \sum x_{i} & \sum 1 \end{array}\right)\left(\begin{array}{c}a\\ b \\ c \end{array}\right) = \left(\begin{array}{c}\sum x^2_{i}y_{i}\\ \sum x_{i}y_{i} \\ \sum y_{i}\end{array}\right)$$
これまた同じように、 \(\left(\begin{array}{c} x_{1}^2 & x_{1} & 1\\ x_{2}^2 & x_{2} & 1\\ : & : & : \\ x_{n}^2 & x_{n} & 1\end{array}\right)\)を \(A\)とし、その転置 \(\left(\begin{array}{c}x_{1}^2 & x_{2}^2 & .. & x_{n}^2\\ x_{1} & x_{2} & .. & x_{n} \\ 1 & 1 & .. & 1\end{array}\right)\) と表現され、\(A^{\top}\)となり、最後\(\left(\begin{array}{c}a \\ b\\ c \end{array}\right)\)を \(x\)とすると、先の式 \(A^{\top}Ax\) と一致する。
2次となり、変数が増えたが、行列表現だと何も変わらない。このあたりが行列のすごいところなのだと思う。がなじめない。もちろん誤差\(Err\)を求める行列式も1次の時と完全に同じ。何次であろうと同じ。
Pythonによる検算
というわけで、検算してみます。Pythonのライブラリを使って求めた、1次、2次の近似の結果と、行列演算で求めた結果が一致するかどうかを確認する。
サンプルコード
import numpy as np from matplotlib import pyplot as plt x = np.linspace(-100,100,201) y = 0.1*x**2 + 35*x + 70 + np.random.randn(201)*45 #近似式 ref1 = np.polyfit(x,y,1) ref2 = np.polyfit(x,y,2) #近似式の計算 y1 = np.poly1d(ref1)(x) y2 = np.poly1d(ref2)(x) #ベクトルの準備 one = np.ones_like(x) X1 = np.stack([x,one],1) X2 = np.stack([x*x,x,one],1) #行列演算での係数算出 invX1 = np.linalg.inv(np.dot(X1.T,X1)) X1tY = np.dot(X1.T,y) ans1 = np.dot(invX1,X1tY) invX2 = np.linalg.inv(np.dot(X2.T,X2)) X2tY = np.dot(X2.T,y) ans2 = np.dot(invX2,X2tY) #グラフに表示 plt.scatter(x,y) plt.plot(x,y1) plt.plot(x,y2) plt.show()
解説
ベースとなる適当な2次曲線に対して、ランダムにオフセットを加えて乱します。
x = np.linspace(-100,100,201) y = 0.1*x**2 + 35*x + 70 + np.random.randn(201)*45
これを入力のデータセットとします。
polyfit
これがnumpyで用意されている多項式近似の関数。あまりに簡単すぎます。この計算結果をそれぞれ、ref1,ref2へ格納し、正解とします。
続いて行列での算出です。
stack
ベクトルデータを作るためのnumpy arrayの並び替え、値追加の関数。横っちょに1を並べています。
linalg.inv
逆行列算出関数。疑似逆行列を求めるpinvを使った方がいいのかもしれませんが、今回は検算が目的なので。これで良しとします。
行列演算
invX1 = np.linalg.inv(np.dot(X1.T,X1)) X1tY = np.dot(X1.T,y) ans1 = np.dot(invX1,X1tY)
ライブラリを使わずとも、この3行で同じ答えが出ました。行列演算おそるべし。そして1次も2次も同じ計算なので、ソースコードもまるで同じ。ちなみにプロットした結果は、
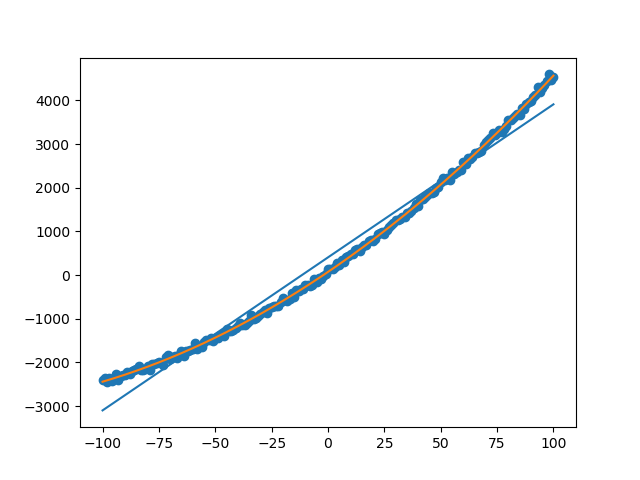
計算結果のref1/2とans1/2は完全一致しました。少なくともデバッガでモニタ出来る桁数の範囲では。
まとめ
何とか高校数学の範囲で、小難しい行列の記述との等価性は確認できました。Pythonでの検算結果もOK。行列演算で表現してしまえば、何次に拡張しても同じ式で表現できてしまうあたり恐ろしい。応用はいろいろできると思います。例えば、
$$ax+by+cz=v$$
のような式で表現される出力vを求める際に、\(x,y,z,v\)のデータセットから、その誤差最小になるような係数\(a,b,c\)を求めよ。みたいな問題も同じ行列式に行き着く。汎用性が高い良い表現手法なのだと思う。がなじめない。
この理解であってるかなぁ。数学出来る人の脳みそはすごいなぁ。数式をLatex表現で書くのも疲れたぁ。ココも頼れたなぁ。



コメント