行列の掛け算による両変換の合成。できるんじゃないかなぁと思ってましたが、やはりできました。そりゃそうですよね。行列使った座標変換なんだし。Python+OpenCVでその動きも確認してみました。
アフィン変換
これまで何気なく使っていましたが、少し真面目に確認してみました。
簡単に言うと、2次元の画像に対して、回転、拡大縮小、シフト、せん断等の、平行四辺形から平行四辺形への座標変換を実現できる幾何変換です。詳細いろいろなサイトで紹介されています。
利点として、同次座標表現にし、3×3行列に拡張することで、行列の積としていろいろな変換を結合することができます。
典型的なのが回転と拡大縮小。加えてシフトも。それぞれの変換行列を作って、その行列の積でそれらの変換の組み合わせができます。
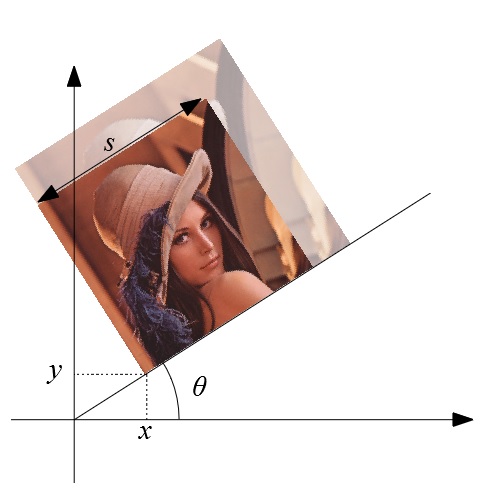
例えば、画像をS倍に拡大(Sc)して、Sx,Syだけ画像をシフト(Sh)した後に、角度θだけ回す(R)。といった変換であれば、それぞれの変換行列を作ってそれを右から並べてあげればそれらを一気に表現した行列になります。
$$Sc = \left( \begin{matrix} s & 0 & 0 \\ 0 & s & 0 \\ 0 & 0 & 1 \end{matrix} \right) \\ Sh=\left( \begin{matrix} 1 & 0 & Sx \\ 0 & 1 & Sy \\ 0 & 0 & 1 \end{matrix} \right) \\ R = \left( \begin{matrix} \cos \theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{matrix} \right)$$
この各行列を
$$\left( \begin{matrix} x’ \\ y’ \\ 1 \end{matrix} \right) = R\cdot Sh\cdot Sc\left( \begin{matrix} x \\ y \\ 1\end{matrix} \right)$$
とした行列を作ってあげると、いっぺんに変換してくれます。
便利です。
python+OpenCVであれば、
cv2.getAffineTransform(src, dst)
を使うことで、srcとdstに対応する3点を指定するだけでその行列を作ってくれます。
cv2.getRotationMatrix2D(center, angle, scale)
を使うことで、回転中心、回転角度、拡大率を指定してその行列を作ってくれます。sin/cosを知っている必要はまるでないです。
射影変換
ホモグラフィー変換とも呼ばれるこの変換。真面目に理解しようとするといっぱい方程式を解かないといけないので大変ですが、アフィン変換同様に3×3の行列で幾何変換してくれます。
アフィン変換では実現できなかった任意の四角形から任意の四角形へ写像できるので、変換の自由度は高いです。斜めから撮影した画像を正面からとらえたような画像へ変換したり、そんな変換でよく使われます。

これも3×3行列です。右下の要素は1固定らしいのでパラメータは8つです。いろいろな式がWeb上にはあって、正直迷いましたが、一番しっくり来た記述は以下でした。(sは変数ではなく、計算すれば求まります。)
$$s\left( \begin{matrix} x’ \\ y’ \\ 1 \end{matrix} \right) = \left( \begin{matrix} H_{11} & H_{12} & H_{13} \\ H_{21} & H_{22} & H_{23} \\ H_{31} & H_{32} & 1 \end{matrix} \right)\left( \begin{matrix} x \\ y \\ 1\end{matrix} \right)$$
やはりOpenCVには便利関数があり、
cv2.getPerspectiveTransform(src, dst)
で、srcとdstに対応する4点を指定して、行列を返してくれます。(この計算結果も行列の最後の要素は1.0でした)
2枚の画像の間の対応点列から、その行列を推定してくれる便利な関数もあります。
cv2.findHomography(srcPoints, dstPoints, ..)
チェッカーパターンでカメラキャリブレーションして(レンズの歪みは非線形なのでこの変換では補正できない。)、こいつで仮想視点へ切り替え。とかそんなアプリケーションで使われます。
車の駐車時に上からの視点にしてくれる(アラウンドビューモニターというらしい)もおそらくこんな感じの事を複数のカメラを使ってしているのだと思われます。
行列による結合
同じように行列演算で変換座標を求める両者なので、結合できるかなぁと思ったらやはりできました。
アフィン変換は射影変換の一部ととらえられそうです。
試しに、4点の対応点から得られた射影行列Hに対して、画像中心から45度回転+1/2縮小を行うアフィン行列Rをかけたうえで射影変換してみました。式にすると
$$s\left( \begin{matrix} x’ \\ y’ \\ 1 \end{matrix} \right) = R\cdot H\left( \begin{matrix} x \\ y \\ 1\end{matrix} \right)$$
pythonコードは
import cv2
import numpy as np
img = cv2.imread("lena.jpg")
h, w = img.shape[:2]
src_pts = np.array([[0,0], [0,h], [w,h], [w,0]], dtype=np.float32)
dst_pts = np.array([[0,0], [50,400], [450,500], [380,30]], dtype=np.float32)
# 適当な射影変換行列
mat = cv2.getPerspectiveTransform(src_pts, dst_pts)
out = cv2.warpPerspective(img, mat, (w, h))
cv2.imwrite("lena2.jpg", out)
# 回転と縮小のアフィン変換行列
mat2 = cv2.getRotationMatrix2D((w//2, h//2), 45, 0.5)
m = np.array([[0.0, 0.0, 1.0]])
mat2 = np.concatenate((mat2, m))
# 行列の掛け算
mat3 = np.dot(mat2, mat)
out = cv2.warpPerspective(img, mat3, (w, h))
cv2.imwrite("lena3.jpg", out)
結果は

射影変換した結果が、45度回って、半分のサイズになっています。
まぁ当たり前なのかもしれませんがね。ちゃんとできました。試しに、上記で作った3×3のアフィン変換行列をwarpPerspectiveで変換させてみたところ、正しくアフィン変換したので、アフィン変換は射影変換の一部ととらえられそうです。
mat2 = cv2.getRotationMatrix2D((w//2, h//2), 45, 0.5)
m = np.array([[0.0, 0.0, 1.0]])
mat2 = np.concatenate((mat2, m))
# 3x3アフィン行列を射影変換
out = cv2.warpPerspective(img, mat2, (w, h))
cv2.imwrite("lena4.jpg", out)
ちょっと曖昧な点がありますが、おおむねあってるかなと思います。



コメント