アフィン変換の変換行列からその回転成分(回転角度、回転中心座標)だけ取り出してみます。ちょっとだけAffine変換の動きを復習したうえで試します。OpenCVとPythonを使います。
Affine変換
アフィン変換そのものの意味については詳細割愛します。画像に対しての、回転と倍率変更、シフトの座標計算を行列で実現してくれる便利な手法です。
回転を実現する座標変換は以下の式で実現できます。いろいろなところで拝見する式です。
$$\left( \begin{matrix} x’ \\ y’ \end{matrix} \right) = \left( \begin{matrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{matrix} \right) \left( \begin{matrix} x \\ y \end{matrix} \right)$$
中学生に戻って簡単に式を図示すると、こんな感じになります。
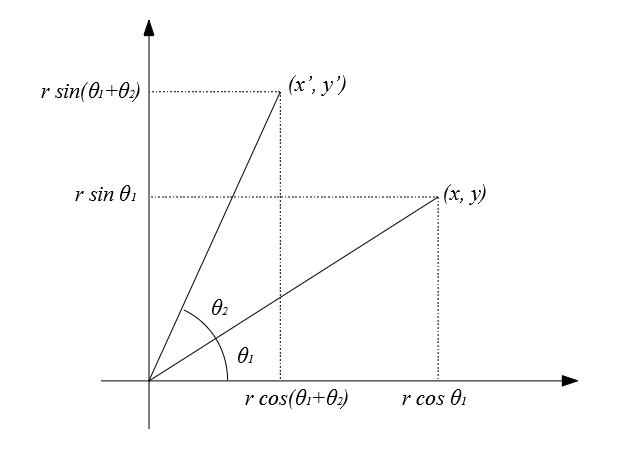
いわゆる加法定理を使って式を分解すると、
$$x=r\cos\theta_{1}\\
y=r\sin\theta_{1}$$
$$x’=r\cos(\theta_{1}+\theta_{2})=r\cos\theta_{1}\cos\theta_{2}-r\sin\theta_{1}\sin\theta_{2}
=x\cos\theta_{2}-y\sin\theta_{2}\\
y’=r\sin(\theta_{1}+\theta_{2})=r\sin\theta_{1}\cos\theta_{2}+r\cos\theta_{1}\sin\theta_{2}
=y\cos\theta_{2}+x\sin\theta_{2}$$
こうなって、上記行列式
$$\left( \begin{matrix} x’ \\ y’ \end{matrix} \right) = \left( \begin{matrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{matrix} \right) \left( \begin{matrix} x \\ y \end{matrix} \right)$$
に戻ります。このアフィン変換で画像は\(\theta_{2}\)だけ回って、
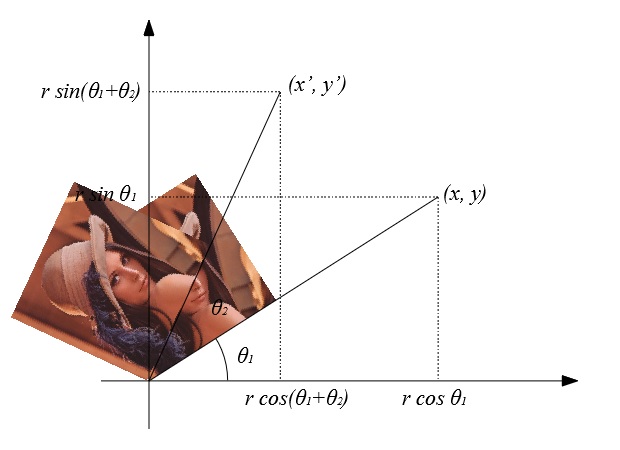
こうなります。
ちなみに倍率変更に関しては以下
$$\left( \begin{matrix} x’ \\ y’ \end{matrix} \right) = \left( \begin{matrix} S_{x} & 0 \\ 0 & S_{y} \end{matrix} \right) \left( \begin{matrix} x \\ y \end{matrix} \right)$$
X方向とY方向それぞれの倍率を指定できます。
この2つの変換式をOpenCV上で簡単に計算してくれる関数が、
cv2.getRotationMatrix2D(center, angle, scale)
で、簡単にAPIを見ると
| center | 入力画像における回転中心のx,y座標 |
| angle | 度単位で表される回転角度.正の値は,反時計回り |
| scale | 等方性スケーリング係数(要は縦横同じ倍率) |
| matrix | 返り値。2×3の出力行列 |
このような感じです。ググって最初に見つかる誰もが見ると思われる公式と思われるドキュメントには
とありますが、ここで示されている式には一部誤りがあります。検算したときにどうにも一致しなくて英語版の方を調べてみると、
間違い探しのようですが、符号が逆です。英語版の方が正しいです。

広く見るいわゆるアフィン変換とはsinの符号が逆ですが、これは回転の正の向きがどちらかの違いだけで、この定義だと反時計回りに正の値を取る仕様になっているようです。
回転の向きはよく見るアフィン変換の向きと同じですが、画像のy座標が、下に向かって正の値を取るので、sinの符号が逆になります。cosは遇関数なので符号は反転しません。
mat = cv2.getRotationMatrix2D((center.x, center.y), angle, scale)
として求めたmatを用いて、あるx,y座標に対して、
x' = x*mat[0, 0] + y*mat[0, 1] + mat[0, 2] y' = x*mat[1, 0] + y*mat[1, 1] + mat[1, 2]
この変換をすると、変換先の座標はx’,y’となります。
この関数による変換は、回転、倍率変更、シフトの3つの変形が組み合わさっています。分解してみると、
1.回転中心位置を原点までシフト
2.回転
3.拡大・縮小
4.原点を中心位置を戻す
の4つの変換をいっぺんにしてくれる行列ということになります。それぞれの式は、
$$Sh_{1}=\left( \begin{matrix} 1 & 0 & -center.x \\ 0 & 1 & -center.y \\ 0 & 0 & 1 \end{matrix} \right) \\ R = \left( \begin{matrix} \cos \theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{matrix} \right) \\ Sc = \left( \begin{matrix} scale & 0 & 0 \\ 0 & scale & 0 \\ 0 & 0 & 1 \end{matrix} \right) \\ Sh_{2} = \left( \begin{matrix} 1 & 0 & center.x \\ 0 & 1 & center.y \\ 0 & 0 & 1 \end{matrix} \right)$$
この4つの行列を右から順に乗じることで、行列の合成ができます。このあたりアフィン変換便利です。
$$\left( \begin{matrix} x’ \\ y’ \\ 1 \end{matrix} \right) = Sh_{2}\cdot Sc\cdot R\cdot Sh_{1}\left( \begin{matrix} x \\ y \\ 1\end{matrix} \right)$$
この4つでそれぞれをx,yに対して順に適用することで、最終的なドキュメントに載っている式に変換されます。この際、便宜上1を加えた同次座標系になっている点ポイントです。シフトを扱うためです。
注意しないといけないのは、変換先の任意のx’,y’の値を求めようとすると、この逆行列を求めてあげる必要があります。
$$\left( \begin{matrix} x’ \\ y’ \\ 1 \end{matrix} \right) = A\left( \begin{matrix} x \\ y \\ 1\end{matrix} \right) \\ A^{-1} \left( \begin{matrix} x’ \\ y’ \\ 1 \end{matrix} \right) = \left( \begin{matrix} x \\ y \\ 1\end{matrix} \right)$$
変換先の任意のx’,y’座標、例えば(0,0)の画素値を求めようとすると、上記式から変換元のx,y座標を特定することができます。画像変換時にはおそらくこの処理してると思います。
以上が簡単なアフィン変換の復習。ちなみにアフィン変換は平行四辺形への変換なので、台形の補正はできません。

その場合は射影変換を使いましょう。
ワープ
この行列に従って画像を変換(ワープ)してくれる関数が、
cv2.warpAffine(src, M, dsize)
です。このAPIは
| src | 入力画像 |
| M | 変換行列 |
| dsize | 出力画像サイズ |
| out | 返り値。変換後の画像 |
となっており、この時、引数として指定する行列は逆行列ではなく、通常の変換行列の方です。なので、シンプルにgetRotationMatrix2Dで求めた通りに画像変換してくれます。
# 中心x,yからangle度、scale倍のaffine行列 mat = cv2.getRotationMatrix2D((x, y), angle, scale) out = cv2.warpAffine(img, mat, (width, height))
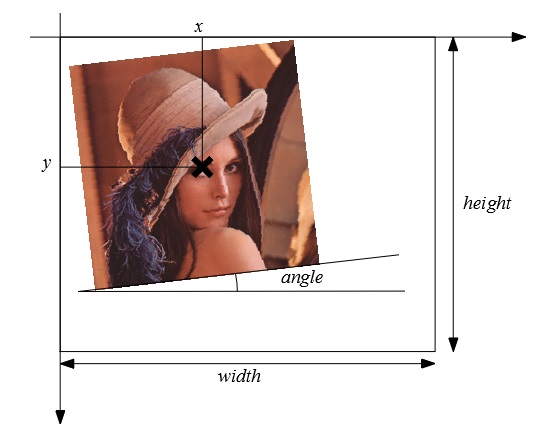
つまり、変換先の値を求めようとするとその逆行列が必要になり、おそらく内部ではまず逆行列を求めた後に、画像変換しているものと思われます。
warpAffineに頼らず、remap関数を使って、自前でその画像変換を書こうと思うと、
# 中心x,yからangle度、scale倍のaffine行列 mat = cv2.getRotationMatrix2D((x, y), angle, scale) inv_mat = cv2.invertAffineTransform(mat)
このように、まず逆行列を求めるステップが必要になります。これになかなか気づけず少しはまりました。warpAffineと答えが逆になったので…。(2倍を指定すると1/2倍が結果として出てくる…)Affine行列の逆行列は
cv2.invertAffineTransform(mat)
で求まってしまいます。なんとも簡単です。
とはいえ逆行列も今回のように小難しく考える必要はなく、2倍の変換の逆は1/2だし、45°回転の逆は-45°回転なので、そのような変換行列をあらかじめ指定すればその通りにしてくれます。
そのうえで、remapを適用します。
X, Y = np.meshgrid(np.arange(width), np.arange(height))
XX = X*inv_mat[0, 0] + Y*inv_mat[0, 1] + inv_mat[0, 2]
YY = X*inv_mat[1, 0] + Y*inv_mat[1, 1] + inv_mat[1, 2]
out = cv2.remap(img, XX.astype('float32'), YY.astype('float32'), cv2.INTER_LINEAR)
このremap関数はこれはこれで幾何変換するのには便利な手段です。ここでAffine変換を題材少し詳細に遊んでいます。(このステップに関しても詳細説明載せています。)
回転成分の抽出
こんなアフィン行列ですが、getRotationMatrix2Dを使って求めるだけではありません。理屈上2枚の画像間で、対応する3点を指定することで、一意にその行列が特定されます。これも関数が用意されています。
cv2.getAffineTransform()
使い方は簡単で、srcの3つの座標セットと、対応するdstの3つの座標セットを指定してあげるとその間の変換行列を作ってくれます。(ちなみに射影変換は4点)
また3つ以上の複数の座標列のセットから変換行列を推定してくれる関数もあります。
cv2.estimateAffinePartial2D()
詳細は割愛しますが、このようにいろいろな形で行列が求められます。
ちなみに逆行列が欲しければ、この変換元と変換先を逆にしておけば求められます。
その中から回転成分だけを取り出す必要があったので、その時のメモを残しておきます。
今回スキューは無視します。倍率変更とシフトは発生しています。スキューが起こっていないないし微小である前提で角度を求めます。
と言ってもやり方は式を見れば一目瞭然で、cosとsinからatanを使って求めるだけです。
$$\tan\theta=\frac{\sin\theta}{\cos\theta}$$
この中学数学でタンジェントを求めることができるので、その時の角度は
$$\arctan=\frac{\sin\theta}{\cos\theta}$$
です。Python上では、
import math : math.atan2(y, x)
で求められるので、これを使うだけです。(今回の場合atanよりatan2の方が便利です。分子が先という点注意が必要です。)
求まった行列の特定の成分から
mat = cv2.getRotationMatrix2D((x, y), angle, scale) da = -math.atan2(mat[1,0],mat[0,0]) #ラジアン s = mat[0,0] / math.cos(da) #拡大率
とするだけで角度(ラジアン)が求められます。(ついでに拡大率も求めています。)符号の定義がややこしいですが、上述したように反時計回りを正とするとこうなります。
ついでに回転中心の座標も求めてみます。ドキュメント記載のgetRotationMatrix2Dで得られる行列

この一見ややこしい式に見えますが、さほど難しくはなく、center.x/center.yは
$$(1-\alpha)\cdot center.x-\beta\cdot center.y=a\\
\beta\cdot center.x+(1-\alpha)\cdot center.y=b$$
この連立方程式を解けば求まります。(ここで、a,bは求まった配列内の値)ここも行列を使って表現した、
$$\left( \begin{matrix} 1-\alpha & -\beta \\ \beta & 1-\alpha \end{matrix} \right) \left( \begin{matrix} center.x \\ center.y \end{matrix} \right)=\left( \begin{matrix} a \\ b \end{matrix} \right)$$
これを、左から逆行列を乗じて解いてやると簡単に求められます。コードにすると
import math import numpy as np import cv2 mat = cv2.getRotationMatrix2D((x, y), angle, scale) da = -math.atan2(mat[1,0],mat[0,0]) #ラジアン s = mat[0,0] / math.cos(da) #拡大率 m = np.zeros([2, 2]) m[0, 0] = 1 - mat[0, 0] m[0, 1] = -mat[0, 1] m[1, 0] = mat[0, 1] m[1, 1] = m[0, 0] mm = np.zeros([2, 1]) mm[0, 0] = mat[0, 2] mm[1, 0] = mat[1, 2] center = np.dot(np.linalg.inv(m), mm) print(scale) print(s) print(angle) print(math.degrees(da)) print(x) print(y) print(center)
角度、倍率、回転中心座標。確かに正しそうです。
以上。アフィン変換とその行列からの回転角および回転中心座標抽出のpythonスクリプトでした。



コメント