立方体の展開図CubeMapから全天球画像(equirectangular)へPython使って変換してみます。このあたりすでにライブラリはあるようなのですが、原理を確認しながら自前で書いてみます。

前回記事の逆変換を行います。
全天球画像とCubeMap
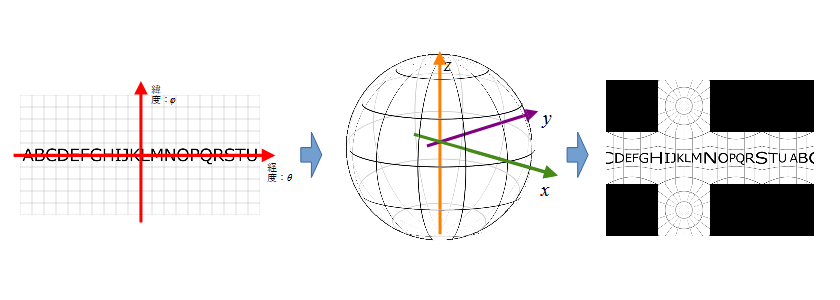
HETAに代表される360度カメラで撮影された画像(正距円筒図法)は、カメラを中心としてぐるっと1周分が1:2の縦横比の画像として記録されています。このフォーマットはいわゆる世界地図と同じように、縦に緯度、横に経度で示した形式になっています。緯度、経度の同じ角度が等間隔になるようにレイアウトされるため、左右に360度、上下に180度、結果として1:2の画像フォーマットになります。

それに対してCubeMapは前後左右上下の6面の2次元の画像を使って表現する方法で、前述のエクイレクタングラー形式と相互変換できます。直感的にはこのフォーマットの方が歪みも少なくわかりやすいですね。

前回記事では全天球画像からCubeMapへ変換してみたので、今回はその逆です。
3次元座標へのマッピング
出力する全天球画像の各座標が半径rの球上のどこにマッピングされるか計算します。緯度経度とx,y,z座標の変換テーブルを作ります。
任意の緯度φ、経度θの座標が3次元の球体のどこへマッピングされるか考えてみます。

球の中心を原点に緯度方向にz軸をとり、経度ゼロ(グリニッジ天文台の経度)をx軸ととると、この図のように任意の点はθとφで特定できる気がします。
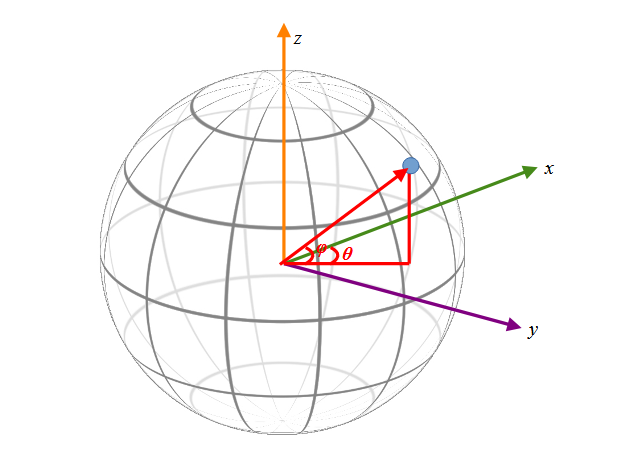
この図をまずはy-z平面へ投影(地球を横から投影)した時のzの値を考えてみます。
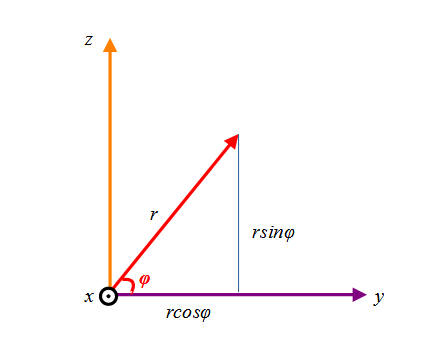
すると半径rの球はz=rsinφへ投影されます。図はちょっと正確ではないです。θ=0の時を例にした図だと思ってください。θが値を持つ場合必ずしもy=rcosφではないですが、zはどんなθでもz=rsinφです。
次にx-y平面に投影(地球を真上から投影)した時のx,yの値を考えてみます。
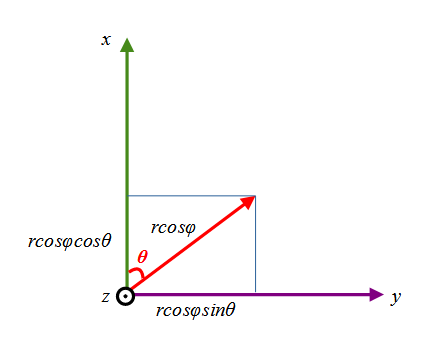
すると投影される長さはrcosφになるので、任意の緯度経度φ、θは、球の中心を原点としたx,y,z座標
$$ x = r\cos\phi\cos\theta \\
y = r\cos\phi\sin\theta \\
z = r\sin\phi$$
にマッピングされることがわかります。今回半径は1で考えるのでr=1で計算します。Pythonで書くと
##
# @brief 3次元座標群取得関数
# @details 360度画像の緯度経度が半径1の球の3次元座標のどこにマッピングされるか
# @param img_w 360度画像の幅
# @param img_h 360度画像の高さ
# @return x,y,zの座標群
def create_3dmap_from_size(img_w, img_h):
h = np.linspace(-np.pi/2, np.pi/2, img_h, endpoint=False)
w = np.linspace(-np.pi, np.pi, img_w, endpoint=False)
# 配列を対称形にするためのオフセット
h = h + (np.pi/2) / img_h
w = w + np.pi / img_w
theta, phi = np.meshgrid(w, h)
x = np.cos(phi) * np.cos(theta)
y = np.cos(phi) * np.sin(theta)
z = np.sin(phi)
return x, y, z
これで任意の画像サイズのφ,θから球上のx,y,zへ対応関係が求まります。
全天球画像への3次元座標からのマッピング
3次元座標x,y,zがCubeMapのどこの面のどこの座標にマッピングされるか計算します。まずは正面から。
これが案外厄介で、球面上のどの範囲が正面に来るのか逆算するのが難しく、ここは開き直ってすべての3次元座標と正面の面の交点を求めて、1辺1の正方形の面を通過する部分だけ選ぶ作戦とします。
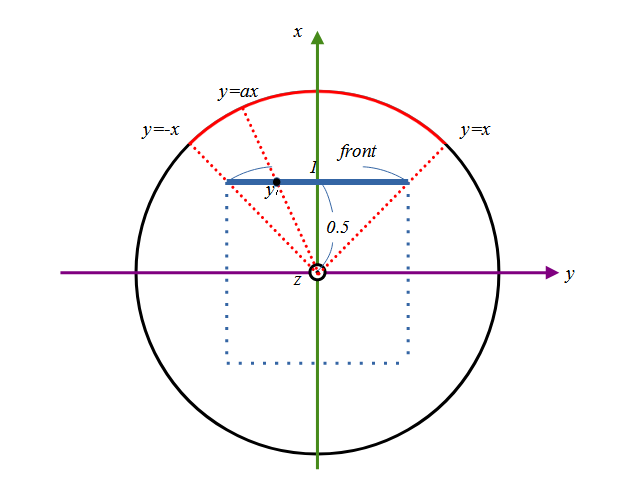
球面上のx,y,zからこの赤い部分に相当する部分だけ選ぶやり方です。x=0.5と直線y=axの交点において、y座標が-0.5~0.5の間、同様にz座標も-0.5~0.5の範囲に来るものだけを選びます。a = y / xとなるので簡単な計算で交点が求まります。
式で表現するよりコードで見た方がピンと来たのでコードで表現します。xx,yyを正面の画像座標系(図中青のfrontの部分)としてこんな感じ。
# front
xx = 0.5 * y / x
yy = 0.5 * z / x
mask = np.where((xx > -0.5) & (xx < 0.5) & (yy > -0.5) & (yy < 0.5) & (x > 0), 1, 0)
tmpx = np.where(mask, xx, 0)
tmpy = np.where(mask, yy, 0)
条件に合致する箇所だけ1が立ったMask配列を作って、その配列で全体をマスクして必要な部分だけ取り出しています。
他の面に関してもx,y,z座標をアフィン変換で回転させても良いのですが、計算量が馬鹿にならないので、軸を切り替えて6回繰り返します。図を書けばどの軸に上下左右が来るかわかると思いますので、割愛。
ここまでの計算でとあるφθの値はx,y,zのどこにあって、それはCubeMap上のどこにある。というルートがたどれるようになります。このルートをたどって画素を補間します。
ここに関してのコードは最後に載せます。(最終的にトリッキーな後処理を入れるので)
のりしろ追加
出力画像の0,0の位置のデータは元の画像のx,yにある。出力画像の0,1の位置はx’,y’にある。という対応関係のマップを作って最後にcv2.remapで画像変換します。
このx,yは必ずしも整数にならないので、周囲の画素を参照してCubicやLinerなどの補間処理して画素値を計算しています。
この計算は周囲の画素に連続性があることが前提になっています。元の画像が普通の2次元画像やエクイレクタングラー画像であれば問題になりませんが、Cube画像のように、面の境界で画素が突然黒のような背景色に変化するような場合、面の境界部分を参照された時に画素として連続しない黒を参照されおかしな画素補間がされてしまいます。
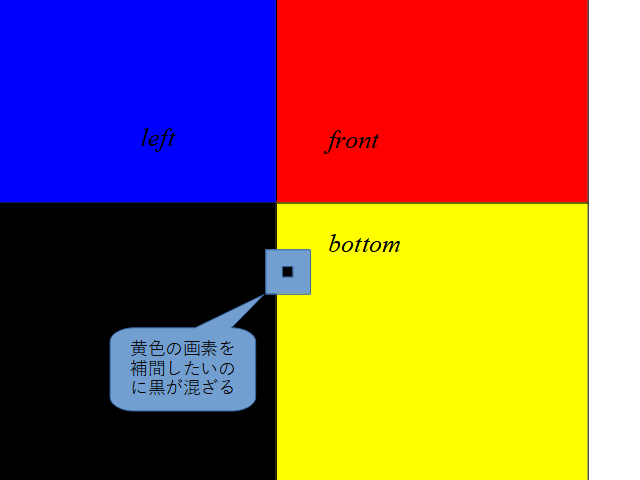
この図を見ていただければ、黄色の画素を補間したいのに、黒が侵入してくることがわかります。この対策をします。CubeMap画像に対して、面の境界でその向こうの画素を持ってきてコピーしときます。事前にCubeMapに加工をしておきます。
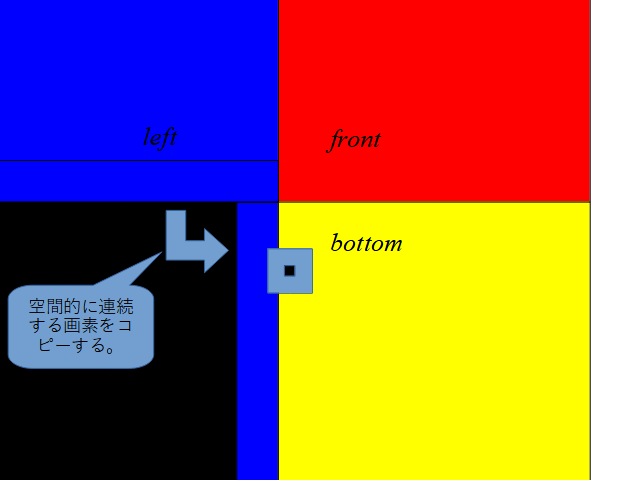
こんな感じで、Cubeの外側に空間的に連続する位置の画素をコピーしておくと、仮に境界部分で外の画素を参照してしまっても、背景の黒が入ってくることはなくなります。このコピーだと立方体の頂点の部分で正確ではないですが、まぁこれくらいはごまかせるでしょう。
Cube全体では、こんな感じでのりしろがつきます。
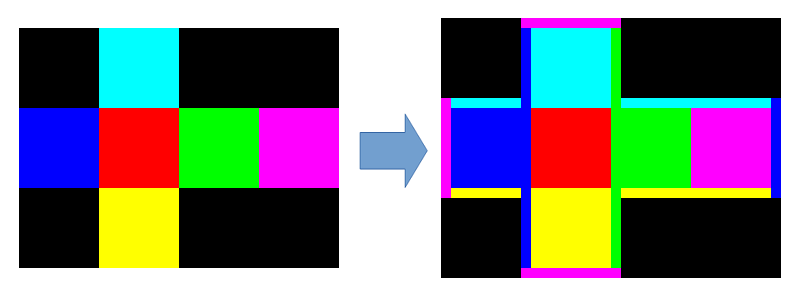
地味にめんどくさい処理できれいなルールは作れず、コードはベタベタな感じです。大事な処理です。
今回はCubic補間にも耐えられるように2画素ののりしろをつけました。デバッグがすげー大変でした。多分大丈夫。
##
# @brief cube画像にのりしろをつける
# @details 画素補間用にcube画像の境界部に2画素分反対側の画像を付与する
# @param img cube画像
# @return のりしろ付き画像
def add_norishiro_to_cube(img):
h,w,c = img.shape
cw = w // 4
# 周囲2画素大きい画像を用意
canvas = np.zeros((h+4, w+4, c), dtype=img.dtype)
canvas[2:-2, 2:-2,:] = img
# 上下左右にのりしろをつける
# up
canvas[0:2,cw+2:2*cw+2,:] = np.rot90(img[cw:cw+2, 3*cw:,:], 2)
# bottom
canvas[-2:,cw+2:2*cw+2,:] = np.rot90(img[2*cw-2:2*cw,3*cw:,:], 2)
# left
canvas[cw+2:2*cw+2,0:2,:] = img[cw:2*cw,-2:,:]
# right
canvas[cw+2:2*cw+2,-2:,:] = img[cw:2*cw,0:2,:]
# 残りの折り返しの部分のコピー
canvas[cw:cw+2,:cw+2,:] = np.rot90(canvas[:cw+2,cw+2:cw+4,:])
canvas[:cw+2,cw:cw+2,:] = np.rot90(canvas[cw+2:cw+4,:cw+2,:],3)
#
canvas[2*cw+2:2*cw+4,:cw+2,:] = np.rot90(canvas[2*cw+2:,cw+2:cw+4,:],3)
canvas[2*cw+2:,cw:cw+2,:] = np.rot90(canvas[2*cw:2*cw+2,:cw+2,:])
#
canvas[cw:cw+2,2*cw+2:3*cw+2,:] = np.rot90(canvas[2:cw+2,2*cw:2*cw+2,:],3)
canvas[:cw+2,2*cw+2:2*cw+4:] = np.rot90(canvas[cw+2:cw+4,2*cw+2:3*cw+4,:])
#
canvas[2*cw+2:2*cw+4,2*cw+2:3*cw+2,:] = np.rot90(canvas[2*cw+2:-2,2*cw:2*cw+2,:])
canvas[2*cw+2:,2*cw+2:2*cw+4,:] = np.rot90(canvas[2*cw:2*cw+2,2*cw+2:3*cw+4,:], 3)
#
canvas[cw:cw+2, 3*cw+2:,:] = canvas[3:1:-1, 2*cw+1:cw-1:-1,:]
canvas[2*cw+2:2*cw+4, 3*cw+2:,:] = canvas[-3:-5:-1, 2*cw+1:cw-1:-1,:]
return canvas
remapを使って変換させようとする以上避けては通れない気がします。
remap
これで、緯度経度(φ,θ)→3次元座標(x,y,z)→CubeMap(x,y)の対応関係が求められ、またこのCubeMapも面境界にものりしろつけたので、remapします。
今回のりしろを2画素つけたので、CubeMap座標には+2のオフセットが必要になります。
Pythonで記述
全コードです。OpenCVは事前に入れといてください。
##
# @brief 3次元座標群取得関数
# @details 360度画像の緯度経度が半径1の球の3次元座標のどこにマッピングされるか
# @param img_w 360度画像の幅
# @param img_h 360度画像の高さ
# @return x,y,zの座標群
def create_3dmap_from_size(img_w, img_h):
h = np.linspace(-np.pi/2, np.pi/2, img_h, endpoint=False)
w = np.linspace(-np.pi, np.pi, img_w, endpoint=False)
# 配列を対称形にするためのオフセット
h = h + (np.pi/2) / img_h
w = w + np.pi / img_w
theta, phi = np.meshgrid(w, h)
x = np.cos(phi) * np.cos(theta)
y = np.cos(phi) * np.sin(theta)
z = np.sin(phi)
return x, y, z
##
# @brief cube画像にのりしろをつける
# @details 画素補間用にcube画像の境界部に2画素分反対側の画像を付与する
# @param img cube画像
# @return のりしろ付き画像
def add_norishiro_to_cube(img):
h,w,c = img.shape
cw = w // 4
# 周囲2画素大きい画像を用意
canvas = np.zeros((h+4, w+4, c), dtype=img.dtype)
canvas[2:-2, 2:-2,:] = img
# 上下左右にのりしろをつける
# up
canvas[0:2,cw+2:2*cw+2,:] = np.rot90(img[cw:cw+2, 3*cw:,:], 2)
# bottom
canvas[-2:,cw+2:2*cw+2,:] = np.rot90(img[2*cw-2:2*cw,3*cw:,:], 2)
# left
canvas[cw+2:2*cw+2,0:2,:] = img[cw:2*cw,-2:,:]
# right
canvas[cw+2:2*cw+2,-2:,:] = img[cw:2*cw,0:2,:]
# 残りの折り返しの部分のコピー
canvas[cw:cw+2,:cw+2,:] = np.rot90(canvas[:cw+2,cw+2:cw+4,:])
canvas[:cw+2,cw:cw+2,:] = np.rot90(canvas[cw+2:cw+4,:cw+2,:],3)
#
canvas[2*cw+2:2*cw+4,:cw+2,:] = np.rot90(canvas[2*cw+2:,cw+2:cw+4,:],3)
canvas[2*cw+2:,cw:cw+2,:] = np.rot90(canvas[2*cw:2*cw+2,:cw+2,:])
#
canvas[cw:cw+2,2*cw+2:3*cw+2,:] = np.rot90(canvas[2:cw+2,2*cw:2*cw+2,:],3)
canvas[:cw+2,2*cw+2:2*cw+4:] = np.rot90(canvas[cw+2:cw+4,2*cw+2:3*cw+4,:])
#
canvas[2*cw+2:2*cw+4,2*cw+2:3*cw+2,:] = np.rot90(canvas[2*cw+2:-2,2*cw:2*cw+2,:])
canvas[2*cw+2:,2*cw+2:2*cw+4,:] = np.rot90(canvas[2*cw:2*cw+2,2*cw+2:3*cw+4,:], 3)
#
canvas[cw:cw+2, 3*cw+2:,:] = canvas[3:1:-1, 2*cw+1:cw-1:-1,:]
canvas[2*cw+2:2*cw+4, 3*cw+2:,:] = canvas[-3:-5:-1, 2*cw+1:cw-1:-1,:]
return canvas
##
# @brief キューブ画像から全天球画像を作る
# @details 6面を展開図から全天球画像へ変換する
# @param img 元となるキューブ(展開図)画像
# @param width 全天球画像の幅(2の倍数である必要がある)
# @return 変換された画像
def cube_to_equirectangular(img, width, interpolation=cv2.INTER_LINEAR):
img_w = width
img_h = width // 2
width = img.shape[1] // 4
x, y, z = create_3dmap_from_size(img_w, img_h)
w = 0.5
# front
xx = w*y / x + w
yy = w*z / x + w
mask = np.where((xx > 0) & (xx < 1) & (yy > 0) & (yy < 1) & (x > 0), 1, 0)
tmpx = np.where(mask, xx*width + width, 0)
tmpy = np.where(mask, yy*width + width, 0)
# back
xx = w*y / x + w
yy = -w*z / x + w
mask = np.where((xx > 0) & (xx < 1) & (yy > 0) & (yy < 1) & (x < 0), 1, 0)
tmpx = np.where(mask, xx*width + width*3, tmpx)
tmpy = np.where(mask, yy*width + width, tmpy)
#right
xx = -w*x / y + w
yy = w*z / y + w
mask = np.where((xx > 0) & (xx < 1) & (yy > 0) & (yy < 1) & (y > 0), 1, 0)
tmpx = np.where(mask, xx*width + width*2, tmpx)
tmpy = np.where(mask, yy*width + width, tmpy)
#left
xx = -w*x / y + w
yy = -w*z / y + w
mask = np.where((xx > 0) & (xx < 1) & (yy > 0) & (yy < 1) & (y < 0), 1, 0)
tmpx = np.where(mask, xx*width, tmpx)
tmpy = np.where(mask, yy*width + width, tmpy)
#up
xx = -w*y / z + w
yy = -w*x / z + w
mask = np.where((xx > 0) & (xx < 1) & (yy > 0) & (yy < 1) & (z < 0), 1, 0)
tmpx = np.where(mask, xx*width + width, tmpx)
tmpy = np.where(mask, yy*width, tmpy)
#bottom
xx = w*y / z + w
yy = -w*x / z + w
mask = np.where((xx > 0) & (xx < 1) & (yy > 0) & (yy < 1) & (z > 0), 1, 0)
tmpx = np.where(mask, xx*width + width, tmpx)
tmpy = np.where(mask, yy*width + width*2, tmpy)
cube = add_norishiro_to_cube(img)
# のりしろ2画素と座標を画素位置に戻すため0.5オフセット
tmpx += (2.0 - 0.5)
tmpy += (2.0 - 0.5)
return cv2.remap(cube, tmpx.astype(np.float32), tmpy.astype(np.float32), interpolation)
この関数を
img = cv2.imread("cube.jpg")
out = cube_to_equirectangular(img, 1920*2, interpolation=cv2.INTER_CUBIC)
cv2.imwrite("eq.jpg",out)
と呼んでやれば

こんな画像が

こんな画像に変換されます。
まとめ
過去の記事の焼き増しの部分も多分にありますが、CubeMapから全天球画像への変換をPython使って試してみました。コードはかなり泥臭い記述になってしまいましたが、この記事と並行して眺めればまぁ何となく思い出せるでしょう。



コメント