全天球画像(equirectangular)を立方体の展開図CubeMapへPython使って変換してみます。このあたりすでにライブラリはあるようなのですが、原理を確認しながら自前で書いてみます。

ちなみにこの逆変換に関してはこちらで。
全天球画像とCubeMap
THETAに代表される360度カメラで撮影された画像(正距円筒図法)は、カメラを中心としてぐるっと1周分が1:2の縦横比の画像として記録されています。このフォーマットはいわゆる世界地図と同じように、縦に緯度、横に経度で示した形式になっています。緯度、経度の同じ角度が等間隔になるようにレイアウトされるため、左右に360度、上下に180度、結果として1:2の画像フォーマットになります。

緯度経度は地球の中心から赤道を向いて、ぐるっと一周する向きが経度、見上げる見下げる角度が緯度になります。いわゆる世界地図ですね。エクイレクタングラー(equirectangular)とかそんな呼び方するようです。
これに対して、同じ360度の画像を表現するCubeMapというフォーマットがあるようです。

これは前後左右上下の6面の2次元の画像を使って表現する方法で、前述のエクイレクタングラー形式と相互変換できます。直感的にはこのフォーマットの方が歪みも少なくわかりやすいですね。
今回はこのCubeMapへの画像変換をトレースしてみます。
全天球画像の3次元座標へのマッピング
以下以前の記事の焼き増しです。
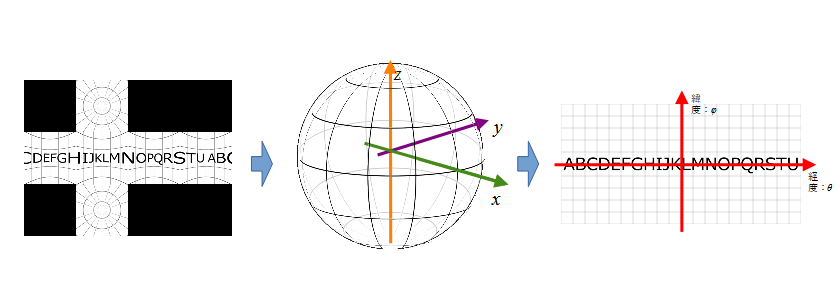
全天球画像画像は緯度経度で画像の縦横が表現されているので、各画素を半径1の球の表面にマッピングすることができます。
任意の緯度φ、経度θの座標が3次元の球体のどこへマッピングされるか考えてみます。

球の中心を原点に緯度方向にz軸をとり、経度ゼロ(グリニッジ天文台の経度)をx軸ととると、この図のように任意の点はθとφで特定できる気がします。
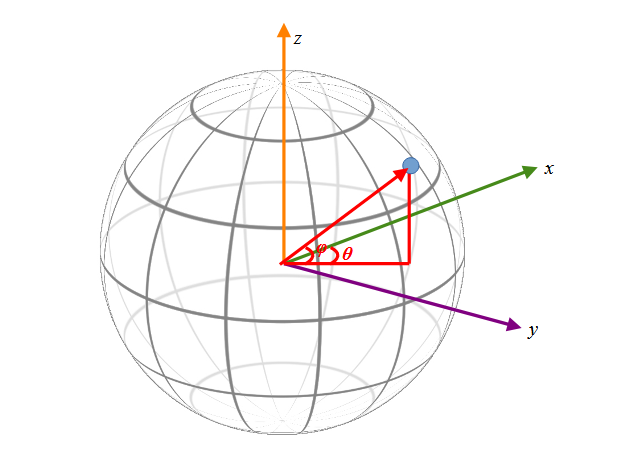
この図をまずはy-z平面へ投影(地球を横から投影)した時のzの値を考えてみます。
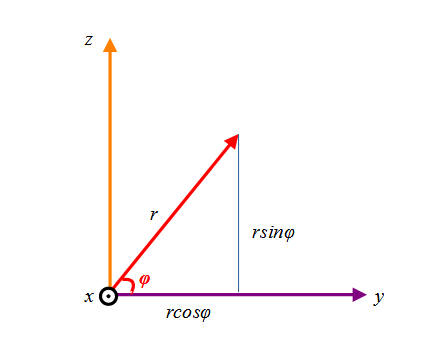
すると半径rの球はz=rsinφへ投影されます。図はちょっと正確ではないです。θ=0の時を例にした図だと思ってください。θが値を持つ場合必ずしもy=rcosφではないですが、zはどんなθでもz=rsinφです。
次にx-y平面に投影(地球を真上から投影)した時のx,yの値を考えてみます。
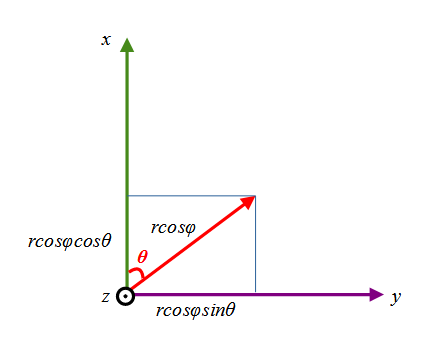
すると投影される長さはrcosφになるので、任意の緯度経度φ、θは、球の中心を原点としたx,y,z座標
$$ x = r\cos\phi\cos\theta \\
y = r\cos\phi\sin\theta \\
z = r\sin\phi$$
にマッピングされることがわかります。半径を1とするとその球面上の任意のx,y,zから、φ、θは
$$ \phi = \arcsin (z) \\
\theta = \arcsin ( \frac{y}{\cos \phi}) $$
と求まります。(x不要ですね)
球面の座標(x,y,z)から元のエクイレクタングラー画像の座標(φ,θ)を求めることができました。Pythonで書くとこんなイメージ。xyz → φθ
##
# @brief 緯度経度群を取得する関数
# @details 半径1の球上の3次元座標群を緯度経度表記に変換する
# @param x x座標群
# @param y y座標群
# @param z z座標群
# @return 緯度、経度群(ラジアン)
def conv_equirectangularmap(x, y, z):
# 緯度・経度へ変換
phi = np.arcsin(z)
theta = np.arcsin(np.clip(y / np.cos(phi), -1, 1))
theta = np.where((x<0) & (y<0), -np.pi-theta, theta)
theta = np.where((x<0) & (y>0), np.pi-theta, theta)
return phi, theta
xが負の時の動作(np.whereの部分)に関しての詳細は上述の以前の記事を見てください。arcsinの値の範囲の問題です。
CubeMapの3次元座標からのマッピング
次にその3次元座標をCubeへマッピングしてみます。今度は前述の半径1の球の中に1辺1の立方体を図のように置きその立方体の各面へ、原点からの写像を考えます。
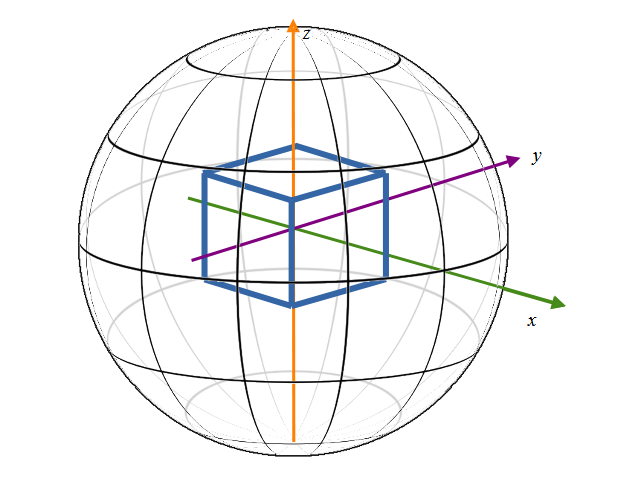
今度はx-y平面で考えます。このx-y平面からxを正の方向にむいた時の面を正面(front)としてその面への球面のx,y,zの値の写像を考えます。
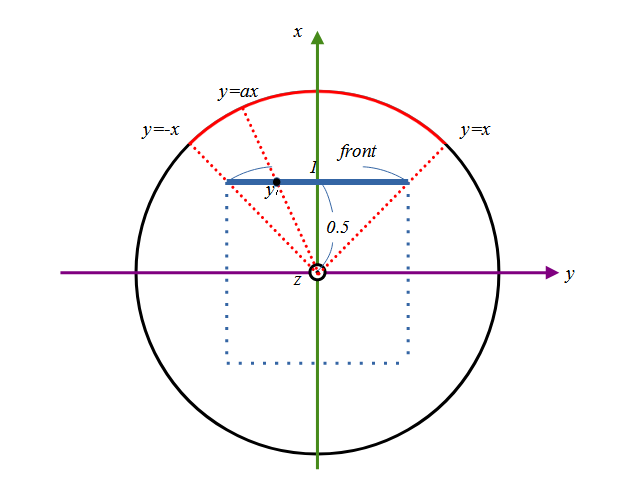
図に示すように、正面のとある\(y1\)の座標は、\(y=a_1x\)と\(x=0.5\)の交点になります。なので式で表すと、
$$ y_1 = a_1 * 0.5 \\
a_1 = 2 y_1 $$
となります。同じようにx-z平面で考えても同様に
$$ z_1 = a_2 * 0.5 \\
a_2 = 2 z_1 $$
となります。この直線と半径1の球との交点を考えます。球の式は
$$ x^2+y^2+z^2=1 $$
となるので、その交点は
$$ x^2+(a_1x)^2+(a_2x)^2=1 $$
$$ x = \sqrt{\frac{1}{1+a_1^2+a_2^2}} $$
と求まります。これにより正面における任意の\(y_1,z_1\)の座標と球面との対応を求めることができます。
これで正面の画像座標(y,z)における球面の座標の対応を求めることができました。先ほどのθφ(すなわち元のエクイレクタングラー画像のx,y)の式との組み合わせで、元のエクイレクタングラー画像の座標まで特定できます。コードにすると
##
# @brief 3次元座標群切り出し関数
# @details とある視点からとある距離の平面を通る半径1の球の表面を結んだ交点座標群を切り出す
# @param img_w 画像の幅(分解能)
# @return x,y,zの座標群
def create_3dmap_to_cube(img_w):
senser_w = 0.5
w = np.linspace(-senser_w, senser_w, img_w, endpoint=False)
h = np.linspace(-senser_w, senser_w, img_w, endpoint=False)
# 配列を対称形にするためのオフセット
w = w + senser_w / img_w
h = h + senser_w / img_w
# センサの座標
ww, hh = np.meshgrid(w, h)
# 直線の式
a1 = 2 * ww
a2 = 2 * hh
# 球面上の3次元座標
x = (1 / (1 + a1**2 + a2**2)) ** (1/2)
y = a1 * x
z = a2 * x
return x, y, z
式の通りに書いているだけです。平面座標x,y → 3次元座標x,y,z
上記2つの関数を続けて呼ぶと、平面座標(Cube正面画像)x,y → 3次元座標x,y,z → 緯度経度(エクイレクタングラー画像)φθと座標が特定できます。
この変換で、

こんな画像(エクイレクタングラー画像)から

こんな画像へ変換できました。これがCubeの正面になります。座標間のマッピングはOpenCVのremap関数を使うと便利です。
##
# @brief 緯度経度情報にしたがって画像を変換する関数
# @details 1:2で格納されている画像から、そのx,y座標を緯度経度と見立てて対応する座標変換を行う
# @param img 元となる360度画像(1:2)
# @param phi 緯度(縦方向 ラジアン)
# @param theta 経度(横方向 ラジアン)
# @return 変換された画像
def remap_equirectangular(img, phi, theta, interpolation=cv2.INTER_CUBIC, borderMode=cv2.BORDER_WRAP):
img_h, img_w = img.shape[:2]
# 画像座標へ正規化(座標を画素位置に戻すため0.5オフセット)
phi = (phi * img_h / np.pi + img_h / 2).astype(np.float32) - 0.5
theta = (theta * img_w / (2 * np.pi) + img_w / 2).astype(np.float32) - 0.5
return cv2.remap(img, theta, phi, interpolation, borderMode = borderMode)
球の回転
続いて右面を同じように求めます。軸となるx,y,zを入れ替えれば同じように求めることができますが、今回は球の回転により求めてみます。図にするとこんな感じ。
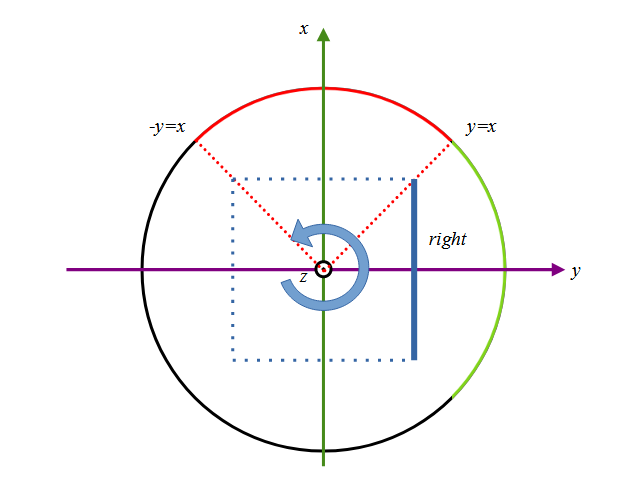
z軸に関して90度球を回転させ、正面に持ってきたのちに先ほどと同じ計算をして右面の画像を作ります。
これも以前の記事で3次元球座標の回転に関してまとめており、その焼き増しです。視点の回転に関しての詳細はこちらの記事にて。
かいつまんで記載すると、いわゆる3次元のアフィン変換を行います。今回右面をまわすので、z軸に関してλ回転する座標は
$$ \left(\begin{array}{c}\cos\lambda & \sin\lambda & 0 \\ -\sin\lambda & \cos\lambda & 0 \\ 0 & 0 & 1 \end{array}\right) \left(\begin{array}{c}x \\ y \\ z\end{array}\right) $$
で表現できます。この式を使って元のx,y,zを座標を回転させることができます。なので、先ほどと同じように、正面の画像座標(y,z)における球面に対応するx,y,zの座標をこの式で回転させ、その回転後のx’,y’,z’から元のエクイレクタングラー画像の座標を求めることで右面の画像を得ることができます。コードにすると
##
# @brief 3次元回転座標を取得する関数
# @details 3次元座標群を原点から指定された角度で回転させる
# @param x x座標群
# @param y y座標群
# @param z z座標群
# @param roll roll角(度単位)
# @param pitch pitch角(度単位)
# @param yaw yaw角(度単位)
# @return 回転後の3次元座標
def rotate_3d(x, y, z, roll, pitch, yaw):
# 回転量
roll = roll * np.pi / 180
pitch = pitch * np.pi / 180
yaw = yaw * np.pi / 180
# 3次元の回転行列
mtx1 = np.array([[1, 0, 0],
[0, np.cos(roll), np.sin(roll)],
[0, -np.sin(roll), np.cos(roll)]])
mtx2 = np.array([[np.cos(pitch), 0, -np.sin(pitch)],
[0, 1, 0],
[np.sin(pitch), 0, np.cos(pitch)]])
mtx3 = np.array([[np.cos(yaw), np.sin(yaw), 0],
[-np.sin(yaw), np.cos(yaw), 0],
[0, 0, 1]])
# 回転行列の積
mtx4 = np.dot(mtx3, np.dot(mtx2, mtx1))
# 座標の行列計算
xd = mtx4[0][0] * x + mtx4[0][1] * y + mtx4[0][2] * z
yd = mtx4[1][0] * x + mtx4[1][1] * y + mtx4[1][2] * z
zd = mtx4[2][0] * x + mtx4[2][1] * y + mtx4[2][2] * z
return xd, yd, zd
同じように回転軸・角度を変えることで残る左、後ろ、上、下も求めることができます。
展開図へのマッピング
このようにして得られた6つの正方形を立方体の展開図の並びで1つの画像にします。
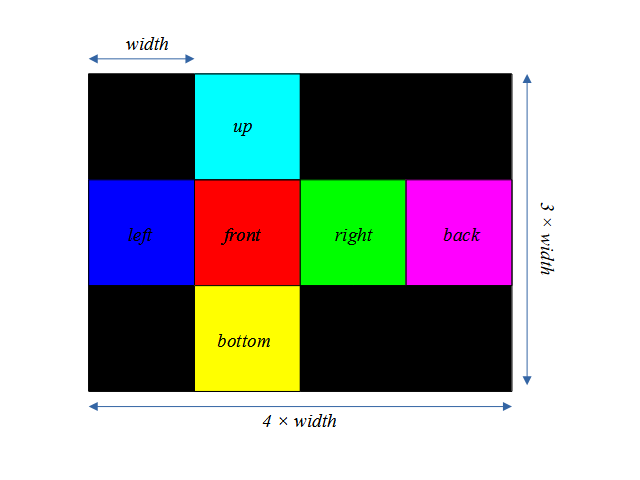
イメージとしてはこんな感じ。この画像が出力されるように画像を並べます。
Pythonで記述
前述の「全天球画像の3次元座標へのマッピング」「CubeMapの3次元座標からのマッピング」「球の回転」「展開図へのマッピング」をそれぞれ関数にしてコーディングしてみます。OpenCVを入れてコピペしてもらえれば動くと思います。
このコードも以前の記事の焼き増し部分が多く入っています。詳細は過去の記事を見てもらった方がいいかもしれません。
##
# @brief 3次元座標群切り出し関数
# @details とある視点からとある距離の平面を通る半径1の球の表面を結んだ交点座標群を切り出す
# @param img_w 画像の幅(分解能)
# @return x,y,zの座標群
def create_3dmap_to_cube(img_w):
senser_w = 0.5
w = np.linspace(-senser_w, senser_w, img_w, endpoint=False)
h = np.linspace(-senser_w, senser_w, img_w, endpoint=False)
# 配列を対称形にするためのオフセット
w = w + senser_w / img_w
h = h + senser_w / img_w
# センサの座標
ww, hh = np.meshgrid(w, h)
# 直線の式
a1 = 2 * ww
a2 = 2 * hh
# 球面上の3次元座標
x = (1 / (1 + a1**2 + a2**2)) ** (1/2)
y = a1 * x
z = a2 * x
return x, y, z
##
# @brief 3次元回転座標を取得する関数
# @details 3次元座標群を原点から指定された角度で回転させる
# @param x x座標群
# @param y y座標群
# @param z z座標群
# @param roll roll角(度単位)
# @param pitch pitch角(度単位)
# @param yaw yaw角(度単位)
# @return 回転後の3次元座標
def rotate_3d(x, y, z, roll, pitch, yaw):
# 回転量
roll = roll * np.pi / 180
pitch = pitch * np.pi / 180
yaw = yaw * np.pi / 180
# 3次元の回転行列
mtx1 = np.array([[1, 0, 0],
[0, np.cos(roll), np.sin(roll)],
[0, -np.sin(roll), np.cos(roll)]])
mtx2 = np.array([[np.cos(pitch), 0, -np.sin(pitch)],
[0, 1, 0],
[np.sin(pitch), 0, np.cos(pitch)]])
mtx3 = np.array([[np.cos(yaw), np.sin(yaw), 0],
[-np.sin(yaw), np.cos(yaw), 0],
[0, 0, 1]])
# 回転行列の積
mtx4 = np.dot(mtx3, np.dot(mtx2, mtx1))
# 座標の行列計算
xd = mtx4[0][0] * x + mtx4[0][1] * y + mtx4[0][2] * z
yd = mtx4[1][0] * x + mtx4[1][1] * y + mtx4[1][2] * z
zd = mtx4[2][0] * x + mtx4[2][1] * y + mtx4[2][2] * z
return xd, yd, zd
##
# @brief 緯度経度群を取得する関数
# @details 半径1の球上の3次元座標群を緯度経度表記に変換する
# @param x x座標群
# @param y y座標群
# @param z z座標群
# @return 緯度、経度群(ラジアン)
def conv_equirectangularmap(x, y, z):
# 緯度・経度へ変換
phi = np.arcsin(z)
theta = np.arcsin(np.clip(y / np.cos(phi), -1, 1))
theta = np.where((x<0) & (y<0), -np.pi-theta, theta)
theta = np.where((x<0) & (y>0), np.pi-theta, theta)
return phi, theta
##
# @brief 緯度経度情報にしたがって画像を変換する関数
# @details 1:2で格納されている画像から、そのx,y座標を緯度経度と見立てて対応する座標変換を行う
# @param img 元となる360度画像(1:2)
# @param phi 緯度(縦方向 ラジアン)
# @param theta 経度(横方向 ラジアン)
# @return 変換された画像
def remap_equirectangular(img, phi, theta, interpolation=cv2.INTER_CUBIC, borderMode=cv2.BORDER_WRAP):
img_h, img_w = img.shape[:2]
# 画像座標へ正規化(座標を画素位置に戻すため0.5オフセット)
phi = (phi * img_h / np.pi + img_h / 2).astype(np.float32) - 0.5
theta = (theta * img_w / (2 * np.pi) + img_w / 2).astype(np.float32) - 0.5
return cv2.remap(img, theta, phi, interpolation, borderMode = borderMode)
##
# @brief 全天球画像からキューブ画像を作る
# @details 半径1の球の中の1辺1の立方体に画像をマッピングさせ、6面を展開図として張り付ける
# @param img 元となる360度画像(1:2)
# @param width 1面の幅
# @return 変換された画像
def equirectangular_to_cube(img, width):
x, y, z = create_3dmap_to_cube(width)
phi, theta = conv_equirectangularmap(x, y, z)
front = remap_equirectangular(img, phi, theta)
x1, y1, z1 = rotate_3d(x, y, z, 0, 0, -90) # 球を左90度まわす
phi, theta = conv_equirectangularmap(x1, y1, z1)
right = remap_equirectangular(img, phi, theta)
x1, y1, z1 = rotate_3d(x, y, z, 0, 0, 90)
phi, theta = conv_equirectangularmap(x1, y1, z1)
left = remap_equirectangular(img, phi, theta)
x1, y1, z1 = rotate_3d(x, y, z, 0, 0, 180)
phi, theta = conv_equirectangularmap(x1, y1, z1)
back = remap_equirectangular(img, phi, theta)
x1, y1, z1 = rotate_3d(x, y, z, 0, 90, 0) # 球を上90度まわす(正面に下が来る)
phi, theta = conv_equirectangularmap(x1, y1, z1)
bottom = remap_equirectangular(img, phi, theta)
x1, y1, z1 = rotate_3d(x, y, z, 0, -90, 0)
phi, theta = conv_equirectangularmap(x1, y1, z1)
up = remap_equirectangular(img, phi, theta)
# 背景となる画像
canvas = np.zeros((width*3, width*4, img.shape[2]), dtype=img.dtype)
canvas[width*1:width*2, :width*1] = left
canvas[width*1:width*2, width*1:width*2] = front
canvas[width*1:width*2, width*2:width*3] = right
canvas[width*1:width*2, width*3: ] = back
canvas[ :width*1, width*1:width*2] = up
canvas[width*2: , width*1:width*2] = bottom
return canvas
こんな関数群を
img = cv2.imread("src.JPG")
cube = equirectangular_to_cube(img, 800)
cv2.imwrite("dst.JPG", cube)
こんなして呼んであげると、

この先ほどのこの画像は

こんな感じに変換されます。なんか合ってそう。
まとめ
基本的には以前まとめたとある視点からエクイレクタングラー画像を眺めた時の画像の生成を6面分繰り返しているだけです。なのでより詳しくは以前まとめた
1.360度写真の平面投影
2.視点の変更と背面の投影
3.視点の回転
を見てください。こちらだといろいろな視点からぐりぐりまわしたものを生成しています。
次はこの逆変換に挑戦してみます。




コメント