
RSA暗号方式。公開鍵暗号で用いられている暗号方式で、電子署名にも使われています。ここまではなんとなく知識として覚えています。そのアルゴリズムを少し読み解いて、なぜこの暗号が強固で使われ続けているのかを掘り下げていきます。
参考図書
この記事の内容は、
この本に書いてある公開鍵暗号の説明内容が個人的にイマイチ理解できなかったので、自分なりに少し掘り下げて考えてみたものになります。
自分はコサインは思いきり人生に関係しています。ただこの本は面白く読むことができました。読書感想文ではないので細かくは語りませんが、数学雑学的なことをわかりやすく解説してくれているとても読みやすい本でした。
基本的にすらすら読めるのですが、第9話の「素数がくれた魔法の鍵」で少し引っかかりました。2つの巨大素数の積から、そのもととなる素数を逆算(素因数分解)できない(逆算するには思いきり時間がかかる)ことをうまく利用し、公開鍵暗号の安全性が保たれている。これを実例を交えて説明してくれています。
このうんちくでとどめてくれていればここまで悩まなかったのですが、暗号の例と解き方の解説をしてくれています。これがすっと落ちてきませんでした。
この部分を少し詳しく考えます。文中の記号、数字は基本的にこの書籍で出てきたものを使っています。
素数の積で割った余りのルール
解説の中では整数\(a\)の\(b\)乗(\(a^b\))をある数\(n\)で割った余りにある一定のルールがあることを説明してくれています。ここである数\(n\)は素数\(p\)および\(q\)の積です。\(n=p\times q\)
例として、3のb乗を33(3×11)で割った余りで説明します。\(3^1\)は3で33で割ると0余り3。\(3^2\)は9で33で割ると0余り9。\(3^3\)は27で33で割ると0余り27。\(3^4\)は81で33で割ると2余り15。と続きます。これを表に表してみると、
3,9,27,15,12,3,9,27,15,12,3,9,27,15,12…
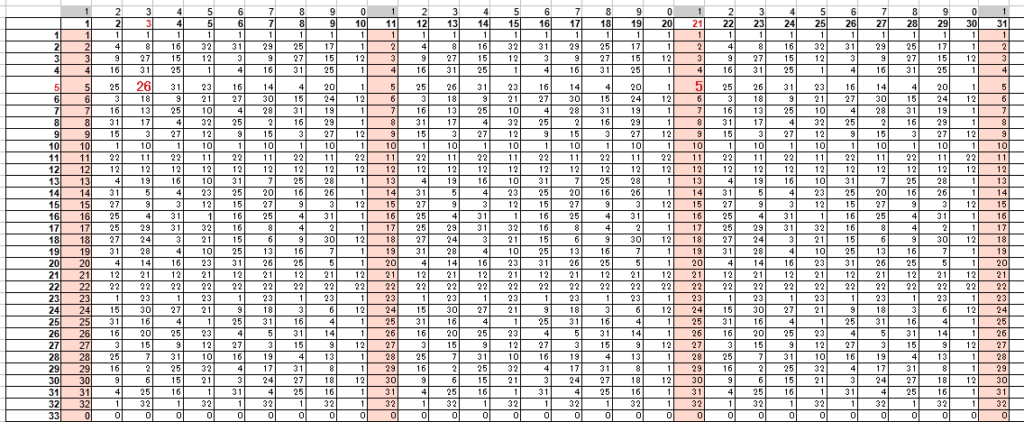
3,9,27,15,12の繰り返しになります。これを3以外も含めた表にすると、書籍の図9-2にある表になります。

こんな感じ。ちなみにエクセルで馬鹿正直に計算させるとあっという間に桁あふれして正しい計算ができませんでした。\(a\)の\(b\)乗なので結構簡単に桁あふれします。なのでこの表をエクセルで作ろうと思うと少し工夫が必要です。これは本筋と関係ないので後回しにします。上記のエクセルはコチラ。任意の素数対でこの表が作れるようになっているハズです。
この33で割った余りに関しては、3以外の他の数すべてが、1乗,11乗,21乗,31乗で繰り返し出てきます。3と11の積である33は、(\((2と10の最小公倍数)\times m+1\))乗で繰り返す。
一般化すると、(\((p-1, q-1の最小公倍数)\times m+1\))乗で繰り返す。だそうです。原理の説明はないのではわかりませんが、\(p\)と\(q\)が素数であることを前提に証明できるのだと思います。誰が気づいたんだかすごいルールです。
この循環するルールがあるために暗号化、復号化が簡単にできてしまいます。
この書籍にはありませんでしたが、軽く調べた感じフェルマーの小定理と呼ばれるもののようです。いったん理解は放棄します。
暗号化と復号化
この前述したルールを利用してデータ5を送る例を示します。この5というデータを公開鍵3および33で暗号化します。
送り手は平文5を3乗して33で割った余り26を暗号文として送ります。この暗号文26から平文5に戻す方法を解説します。
受け手だけが33は3×11であることを知っています。送り手もこの事実は知りません。これが秘密鍵になります。
3と11なので先ほどのように、2と10の最小公倍数10の倍数に1を足した数で循環します。1,11,21,31乗で値が繰り返すルールを求めることができます。公開鍵3乗で暗号化しているのだから、受け手はこの値をあと7乗すれば21乗となることがわかります。(送り手含めた他の人にはそれはわかりません。)なので、送られてきた26を7乗して33で割った余りが答えとなります。Xを復号したいので、計算としては
$$X^{21} \bmod 33 = (X^3)^7 \bmod 33 \equiv 26^7 \bmod 33 = 5$$
ちなみに\(\bmod\)は左辺を右辺で割った余り(剰余)という記号です。\(\equiv\)は合同。めでたく暗号文からX=5が復号されました。
もちろん26を17乗して51乗にしてもよいはずです。
二項定理
ここがすっと入ってこなかったポイントです。なぜ余りである26を7乗してから33で割った余りが、5の21乗を33で割った余りと同じになるかわかりませんでした。
$$(5^3)^7 \bmod 33 \equiv 26^7 \bmod 33$$
この部分。書籍では説明がはしょられています。ただ簡単に二項定理で説明できます。
暗号文26は平文5の3乗を33で割った余りです。商をmとして式にすると
$$ 5^3 = 33 \times m + 26 $$
となります。なので、5の21乗は
$$ 5^{21} = (5^3)^7 = (33 \times m + 26)^7 $$
となります。この\((33 \times m + 26)^7\)を33で割った余りの求め方ですが、この式を展開するとわかりますが、1項除いてすべての項に33がかかってきます。それらの項はすべて33の倍数(余りゼロ)になるわけです。わかりやすく2乗で書くと、
$$ (33 \times m + 26)^2 = (33 \times m)^2 + 2 \times 33 \times m \times 26 + 26^2 $$
いわゆる二項定理というやつです。この値を33で割った余りは、\(26^2\)を33で割った余りと等しくなります。
同様に\((33 \times m + 26)^7\)を33で割った余りは、\(26^7\)を33で割った余りと等しくなります。なので送られてきた暗号文を7乗してから33で割った余りを求めることで、5が復号できるようになります。
このルールがわからないとこの問題は解けません。
安全性
今回は33という小さな素数の積で話をしましたが、これが桁数の多い素数積だと答えを出すことが困難です。
247867
これは何と何の積でしょうか?わかりません。でも
311×797
これはいくつでしょう?これは簡単ですね。なので247867を公開しても、311と797がバレない。この理屈で安全が成り立っています。
推薦図書
ここで深追いした公開鍵暗号の他にもいろいろ面白数学ネタがいろいろ書かれています。基本的にはわかりやすく一気に読めてしまいます。公開鍵暗号だけです。引っかかったの。
この書籍では挿絵を使っていろいろ丁寧に説明がされています。
素数つながりでいえば素数ゼミの話など初めて知りました。他にも対数の使いどころや、円周率が3だったらどうなるとか、それこそサインコサインの有用性までわかりやすく解説されています。さすがに虚数はどうにもならなかったようです。
特に何かの勉強として読むわけでもなく、クイズ番組付けたら役に立ったし意外と面白かった。そんな感じ。
「マンガ」とありますが、息抜き程度にマンガがある程度でほとんどは文章になっています。
おまけ:エクセルでの表の作り方
前述したようにxのy乗を求めると、数十のレベルで簡単に桁あふれします。エクセルで計算できません。なのでこの表はとなりのセルから計算で求めるように作っています。
Aのm乗に対するnの剰余を\(B_{m}\)とすると
$$B_{m} = A^m \bmod n$$
この時商をiとすると
$$A^m = n \times i + B_{m}$$
となる。同様に\(B_{m+1}\)は
$$ B_{m+1} = A^{m+1} \bmod n = A \times A^m \bmod n = A \times (n\times i + B_{m}) \bmod n $$
となり
$$B_{m+1} = A\times B_{m} \bmod n$$
が求まる。すなわち隣の計算結果をA倍してnの剰余を出せばいいことがわかります。このルールで計算すれば桁あふれせず表を作ることができます。


コメント