いわゆるHello World的なことをするための覚書。前回環境づくりからとりあえず動くところまで試したので、続きになります。
環境作りや最小コードは以下です。
今回はいろいろニューラルネットワークの代表的なパラメータをいじってみます。
ネットワーク層
入力層と出力層の間にある隠れ層の数やユニット数を自由に設定できます。数を多くすることによって複雑な問題も解くことができるようになることが期待できます。
ただ隠れ層の数が多いと重みの調整の難易度が上がって学習の進行しにくく、また過学習を起こしやすくなったりします。適切なサイズを指定することになります。
記述は
model.add(Dense(128))
こんな感じ。この場合ユニット数(ノード数)128の層を1層はさんだよ。ってことになりこれを複数層繰り返し書きます。書く順で構造が決まります。
ドロップアウト
ドロップアウトは、過学習を防ぐための手法の一つです。
ランダムにニューロンを削除(0で上書き)し、学習を繰り返します。これにより特定のニューロンに依存せず、より汎用的な特徴を学習するようになります。
ドロップアウトの記述は
model.add(Dropout(rate=0.5))
こんな感じ。rateは比率(この場合5割)。この比率やどこに挟むかがパラメータになります。
活性化関数
全結合層などの演算の後に適用する関数で、ニューロンを活性化させます。
基本的な演算だけだと、入力を線形変換して出力することになりますが、非線形な活性化関数を使うことで非線形性をもたせることができます。
いくつか種類はありますが、代表的なものとしてシグモイド関数やrelu関数などがあります。ちなみにこの関数は微分可能である必要があります。でないと勾配を求められず最適化ができないから。
シグモイド関数は、値が0~1に制限されるので、極端な値が出にくい。
逆にrelu関数はその制限がないので、極端な値になりえます。今回の例題だとreluは向かなそうです。
記述は
model.add(Activation("sigmoid"))
層の間で定義してやります。
損失関数
学習時に出力と正解との差を評価する関数です。0/1の正解率ではなく、出力データと正解データの差を計算して誤差を出します。
損失関数には多くの種類がありますが、二乗誤差やクロスエントロピー誤差など代表的です。
また、学習時この損失関数の微分の計算(勾配を求める)を誤差逆伝播法という手法で行い、出力データと正解データの差を最小化するように各層の重みを更新します。
二乗誤差は出力と正解の差の二乗和を求めて、これを最小化する方法。クロスエントロピー誤差はlogが出てくるちょっとややこしい式で、分類問題よく登場します。
記述は
model.compile(optimizer=sgd, loss="categorical_crossentropy", metrics=["acc"])
compile時の引数で与えるようです。
最適化関数
損失関数を各重みで微分した値から各重みを更新します。どのようにはlossを最小化するように更新するかを決めるのが最適化関数です。
やり方はいろいろあるようですが、最急降下法、SGDやAdamなどのキーワードでググってください。自分も理解しきってないです。基本的には微分して勾配を求めて傾きがしたに向いた方(谷に向かって)重みを更新します。
記述は
sgd = optimizers.SGD(learning_rate=0.01) # 学習率0.01
こんな感じ(これはSGDの例)
学習率
重みをどの程度反映させるか決めるのがこの学習率になります。微分してゼロになると推定された位置に対してどの程度その値を信じるかを設定するもので、1が最大。
全力で信じ切ると値が振幅してしまうので適切に設定してやる必要があります。
記述は前項でネタバレしてますが、
sgd = optimizers.SGD(learning_rate=0.01) # 学習率0.01
こんな感じ(これはSGDの例)デフォルトが0.01で今回の結果もいい感じなので、1%程度しか更新に使わないんですねぇ…。
ミニバッチ
モデルに対して一度に複数のデータを入力して重みの更新をする手法です。このデータ数をバッチサイズと呼びます。
モデルは複数のデータごとに損失関数の値と勾配を計算し、その平均値をもとに1度だけ重みの更新をします。なので高速化しまた特異なデータの影響をはじくことができます。
学習データに偏りがなく、計算資源が多ければ1を設定し、学習データにノイズを含むような場合にはある程度数を多くすることになります。
記述は
history = model.fit(X_train, y_train, batch_size=32, epochs=5, verbose=1, validation_data=(X_test, y_test))
ここの引数batch_sizeになります。
反復
同じ学習データで何回学習するかを設定するものです。あまり多くしすぎてもその学習データに特化した過学習を起こしてしまうので適度に。
この回数をエポック数という言い方をします。
記述はやはりネタバレしてますが、
history = model.fit(X_train, y_train, batch_size=32, epochs=5, verbose=1, validation_data=(X_test, y_test))
ここの引数epochsになります。
Hello Tensorflow World
前回のコードに対して上記で上げたそれぞれのパラメータを適当に反映させてみます。ちょっと長くなりました。
from tensorflow.keras.datasets import mnist
from tensorflow.keras.layers import Activation, Dense, Dropout
from tensorflow.keras.models import Sequential
from tensorflow.keras.utils import to_categorical
from tensorflow.keras import optimizers
import matplotlib.pyplot as plt
import numpy as np
# 画像と正解ラベルの読み込み(訓練データ60000枚とテストデータ10000枚)
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# test data 6枚だけ画像の表示
fig = plt.figure()
for i in range(6):
fig.add_subplot(2,3,i+1)
plt.imshow(X_test[i], cmap = "gray")
# 画像データの並び替え(60000x28x28 -> 60000x784x1)
X_train = X_train.reshape(X_train.shape[0], 784)
X_test = X_test.reshape(X_test.shape[0], 784)
# 正解ラベルの変換(one-hotベクトル化)
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)
# レイヤを順繰りに連続的に重ねる
model = Sequential()
model.add(Dense(256, input_dim=784)) # 1層目 画像が784画素あるので全部入力するとこのサイズ
model.add(Activation("sigmoid")) # 活性化関数はsigmoid
model.add(Dense(128)) # 2層目
model.add(Activation("sigmoid"))
model.add(Dropout(rate=0.2))
model.add(Dense(10)) # 3層目 10クラスに分けるので最終層は10
model.add(Activation("softmax")) # 最終層はsoftmax(合計1の確立表現させるため)
# optimizer:sgd 確率的勾配降下法
sgd = optimizers.SGD(learning_rate=0.01) # 学習率0.01
# loss 損失関数:categorical_crossentropy (多クラス分類問題の正解データ(ラベル)を、one-hot表現(one-hotベクトル)で与えている場合に使用)
# metrics 評価関数:ひとまず自動acc
model.compile(optimizer=sgd, loss="categorical_crossentropy", metrics=["acc"])
history = model.fit(X_train, y_train, batch_size=16, epochs=5, verbose=1, validation_data=(X_test, y_test))
# テスト結果
score = model.evaluate(X_test, y_test, verbose=0)
print("evaluate loss:", score[0])
print("evaluate acc:", score[1])
# 推論結果
result = model.predict(X_test[:6], batch_size=None, verbose=0, steps=None)
print("推論結果:" + str(np.argmax(result, axis=1)))
#accのプロット
plt.figure()
plt.plot(history.history["acc"], label="acc", ls="-", marker="o")
plt.ylabel("accuracy")
plt.xlabel("epoch")
plt.legend(loc="best")
plt.show()
これを実行すると
Epoch 1/5 3750/3750 [==============================] - 5s 1ms/step - loss: 0.8728 - acc: 0.7692 - val_loss: 0.3939 - val_acc: 0.9050 Epoch 2/5 3750/3750 [==============================] - 5s 1ms/step - loss: 0.3998 - acc: 0.8906 - val_loss: 0.3048 - val_acc: 0.9174 Epoch 3/5 3750/3750 [==============================] - 5s 1ms/step - loss: 0.3423 - acc: 0.9049 - val_loss: 0.2796 - val_acc: 0.9214 Epoch 4/5 3750/3750 [==============================] - 5s 1ms/step - loss: 0.3132 - acc: 0.9111 - val_loss: 0.2611 - val_acc: 0.9277 Epoch 5/5 3750/3750 [==============================] - 5s 1ms/step - loss: 0.2929 - acc: 0.9167 - val_loss: 0.2370 - val_acc: 0.9315 evaluate loss: 0.23699785768985748 evaluate acc: 0.9315000176429749 推論結果:[7 2 1 0 4 1]
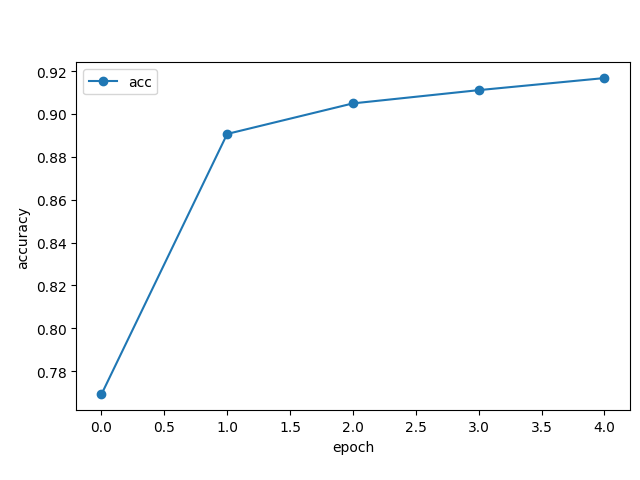
グラフを見るとEpoch数が進むにつれて次第にaccuracyがよくなっていきます。ひとまず93%の正答率で、テスト結果も同93%。いい感じで汎化できてそうです。
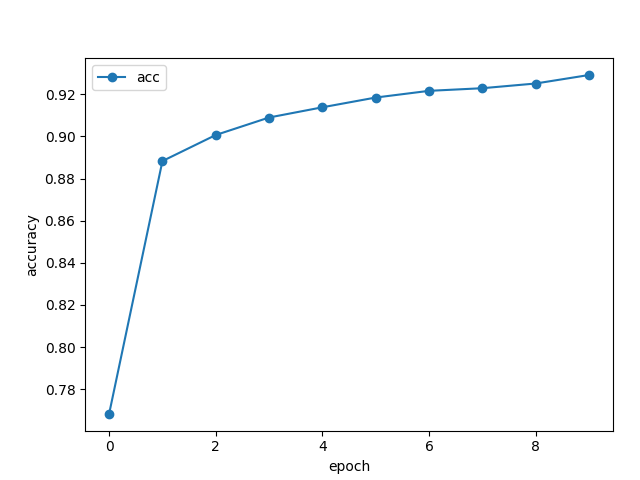
もう少し頑張れそうなので試しにepoch数を10にしてみましたが、94%までは伸びました。
Epoch 10/10 3750/3750 [==============================] - 4s 1ms/step - loss: 0.2403 - acc: 0.9292 - val_loss: 0.2026 - val_acc: 0.9404 evaluate loss: 0.20255783200263977 evaluate acc: 0.9404000043869019 推論結果:[7 2 1 0 4 1]
推論の結果も、入力の画像が

に対して、結果が
推論結果:[7 2 1 0 4 1]
なので私の認識結果と一致します。
コードの解説
パラメータの設定に関しては上記で説明したものをそれぞれ設定しているだけなので割愛。
ややトリッキーなところだけ解説
result = model.predict(X_test[:6], batch_size=None, verbose=0, steps=None)
print("推論結果:" + str(np.argmax(result, axis=1)))
ここで先頭6つ分の推論結果を格納していますが、返り値resultは認識結果というよりは、推論の結果各文字の文字らしさ率を格納している配列になります。
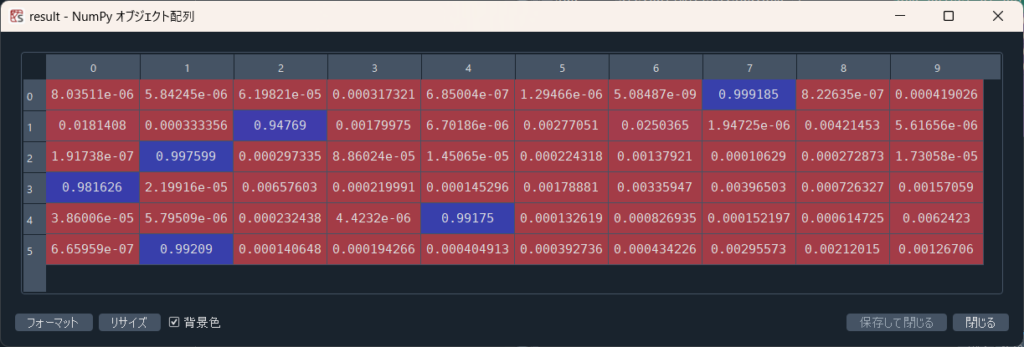
なので最も数字の高い位置(index)が認識された数字になります。今回の場合だと7,2,1,0,4,1の順でどれも90%以上でその数字だと推論しているのであまり迷いはなさそうです。
2だけ94%と低めですね。
np.argmax()
を使って、各行での最大値を持つindexを返しているので、認識された数字がわかるということですね。
しかしnumpyはこんな関数も用意しとるんだな。
いったん様子が分かった気になりました。次はCNNを使ってみます。




コメント