拡大、縮小等、任意の画像幾何変換をやってくれるOpenCVのremap関数を使って、ずれのある2枚の写真の位置合わせをしてみたいと思います。Python使います。

OpenCV.remap
拡大、縮小、回転、シフト等のアフィン変換や射影変換から、レンズの歪み補正等のいわゆる画像幾何変換。そのあたりひっくるめて変換元座標と変換先座標列(map)としてとらえることで、任意の画像幾何変換をやってくれる関数が、OpenCVのremap関数です。
過去、超広角レンズの歪み補正を試みた際にも使いました。
詳細仕様はこちらに任せますが、
簡単にAPIを眺めてみると、
dst = cv.remap( src, map1, map2, interpolation)
となっており、入出力は
| src | 入力画像(変換元画像) |
| map1 | X座標方向のマップ (float32 or 16) |
| map2 | Y座標方向のマップ (float32 or 16) |
| interpolation | 画素補間手法 (cv2.INTER_LINEAR, cv2.INTER_CUBIC とか) |
| dst | 出力画像(変換先画像) |
のようです。くせはなく直感的です。入力の座標と出力の座標を対として保持したテーブル(map)を指定するだけで画像変換してくれます。画像の外の値をどうするだとか、そういったオプションも用意されています。
mapとは出力先の各座標が入っていて、例えば無変換の4×4のX座標は、
[0, 1, 2, 3], [0, 1, 2, 3], [0, 1, 2, 3], [0, 1, 2, 3]
な具合です。左上を原点とした2倍拡大であれば
[0, 0.5, 1, 1.5], [0, 0.5, 1, 1.5], [0, 0.5, 1, 1.5], [0, 0.5, 1, 1.5],
な感じで、各座標位置に変換元座標のどこの座標を参照するかが配列で指定されています。小数点が扱えるので、サブピクセル単位で指定することができます。Y座標に関しても同様で、
[0, 0, 0, 0], [0.5, 0.5, 0.5, 0.5], [1, 1, 1, 1], [1.5, 1.5, 1.5, 1.5]
とすれば同じように2倍です。remap関数で間を補間してくれるのでとても助かります。
map1はx,yを併記した3次元配列で指定することで、map2を省略(None)することも可能なようです。
このremapを使うことで、アフィン変換も実現できます。
通常は
out = cv2.warpAffine(img, matrix, ..)
で一発で済ませると思いますが、回りくどく
matrix = cv2.invertAffineTransform(matrix) X, Y = np.meshgrid(np.arange(w), np.arange(h)) XX = X*matrix[0, 0] + Y*matrix[0, 1] + matrix[0, 2] YY = X*matrix[1, 0] + Y*matrix[1, 1] + matrix[1, 2] out = cv2.remap(img, XX, YY, ..)
としても同じ答えが出るはずです。(厳密には得られたアフィン行列の逆行列を使う必要があります。)meshgridの説明の詳細は割愛しますが、この場合は画像と同じサイズの座標列がX方向とY方向で作られています。
X = [[0,1,2,3,..w-1],
[0,1,2,3,..w-1],
:
[0,1,2,3,..w-1]]
Y = [[0,0,0,0,..],
[1,1,1,1,..],
:
[h-1,h-1,h-1,h-1,..]]
この座標列に対して、行列を乗じていることで、参照すべき座標を得ています。
余談ですが、座標の値を参照するだけのニアレストネイバーであれば、間を補間する計算が必要が無いので、intにして隅っこをクリッピングしたうえで、以下のコードでも同じ意味になるはずです。remap使うより少し速いかも。
XX = np.clip(XX.round().astype(np.int32), 0, w-1) YY = np.clip(YY.round().astype(np.int32), 0, h-1) out = img[(YY, XX)]
remapのメリット
幾何変換に対して回りくどくremapを使う場合、何がうれしいかですが大きく3つ思いつきました。
座標の再計算の軽減
同じ変換を複数の画像に適用する際に、座標の再計算を行わず、mapの使いまわしができるようになります。
affine変換程度であればその恩恵は少ないかもしれませんが、複雑な演算を要求するような幾何変換を、複数の画像に対して適用する場合には、処理速度の点で恩恵があると思います。
先のレンズ歪み補正なんかは先にマップを作っておいた方が有利だと思います。
複数回の変換に伴う画質劣化の軽減
複数の幾何変換処理を、多段で処理する際に補間演算を減らせます。ある変換を示したmapに対してさらに演算をすることで新しいmapを作ることができます。
例えばレンズ歪み補正を行ったmapに対して、さらにAffine変換を追加する際など、画像を2回変換するよりも、画素値の内装(CUBICとか)による画像劣化(おもにボケ)を最小限にすることができます。
画像内で複数変換の組み合わせ
画像内で異なる複数の幾何変換を組み合わせて行うことができるようになります。1つの画像内では1つの変換を行うのがオーソドックスです。Affine変換であればその行列は1つでその行列を使って画像全体を変換すると思います。そうではなく、画像内で異なる変換(Affine変換であれば異なる変換行列を使うとか)を行うような場合、先にマップを作ってから処理した方が便利な場合があります。
場所によって異なるAffine変換をするケースで以下に例示します。
Affine変換行列の結合
Affine変換は行列要素の掛け算、足し算で済んでしまう、いわゆる線形結合で出力座標を計算します。
これは少し便利で、10°回転するAという行列と、-10°回転するBという行列を単純に値を平均すると無回転の行列になります。最もcos、sinの平均値なので必ずしも角度の平均にはなりませんが。
これを応用すると、例えば左半分は左に10°、右半分は右に10°というアフィン行列を2つ作って、その間を線形補間することで緩やかに画像が変化するmapが作れます。コードにすると
h, w = img1.shape[:2] mat1 = cv2.getRotationMatrix2D((w / 4, h / 2), -10, 1) mat2 = cv2.getRotationMatrix2D((w*3 / 4, h / 2), 10, 1)
こんな感じ。mat1が左側半分画像の中心から-10°の回転。mat2が右側半分画像の中心から10°の回転。(厳密にはその逆行列)そんな2つの行列を
affinarray = np.stack([mat1, mat2]) affinarray = affinarray.reshape(1,2,6) affinarray = cv2.resize(affinarray, dsize=(w, h))
このようにしてくっつけて、リニア補間を使って画像と同じ大きさまで拡大(resize)したうえで、先ほどと同じように
X, Y = np.meshgrid(np.arange(w), np.arange(h))
XX = X*affinarray[:,:,0] + Y*affinarray[:,:,1] + affinarray[:,:,2]
YY = X*affinarray[:,:,3] + Y*affinarray[:,:,4] + affinarray[:,:,5]
img = cv2.remap(img1, XX.astype('float32'), YY.astype('float32'), cv2.INTER_CUBIC)
としてあげると、左側は左に回転、右側は右に回転したような、扇型に変換された画像を作ることができます。

この入力画像から

こんなのが作れます。ちょっとresize関数の外挿がおしいので、左右の1/4の領域でイマイチですが、おおよそ予想通りの出力です。
拡大縮小も同じです。
mat1 = cv2.getRotationMatrix2D((w / 4, h / 2), 0, 1) mat2 = cv2.getRotationMatrix2D((w*3 / 4, h / 2), 0, 2)
とすれば、
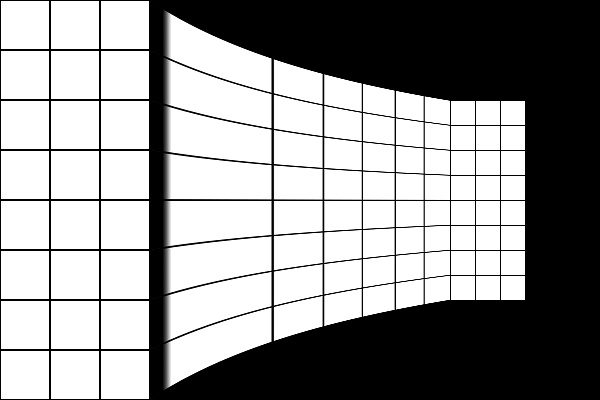
こんな感じ。左半分からじょじょに右に向けて画像が縮んでいきます。やはり左右1/4はおしい。
ここでは説明の都合上アフィン行列をのものを使いましたが、厳密には逆行列を求めてそれを適用する必要があります。なので2倍を指定すると得られる座標は1/2倍されています。
応用(画像位置合わせ)
上記で試したように、複数のAffine変換列を組み合わせることで、動きが無い物体(剛体)を撮影した2枚の写真の位置合わせをしてみます。この間手振れがある前提です。
例えばこんな2枚。シフトと若干の回転を補正すればうまく行きそうなもんですが、そうもいきません。

単純な1つの行列を使った変換では、レンズの歪みや手振れの具合によっては合いきらないことがあります。試してみるとこんな感じ。

画像中心こそ位置が合って動きがほとんどありませんが、画像の外側はうまく行ってません。奥行き方向にも手振れている可能性もあります。ちなみにiPhoneSE(初代)です。これを先ほどのAffine変換の組み合わせを応用してやっつけます。
作戦としては、画像を複数のエリアに分割します。例えば4×4のエリア。そのエリアごとに2枚の画像間で対応点を取ります。これにはAKAZEを使います。AKAZEによる対応点探索に関しての詳細は割愛します。2枚の画像の特徴の似た座標のペアが取れる。と思ってください。コードも、ほぼどこかからの引用です。
結果16セットの対応点が作れます。

この16セットの対応点から16個のAffine変換行列を推定します。Affine行列の推定には、
cv2.estimateAffinePartial2D(pt2, pt1)
これを使います。これまた詳細は割愛。便利にAffine行列を推定してくれます。
これで4×4のエリア毎のAffine行列が作れます。

これを画像と同じサイズにリニアに拡大します。
以下のコードではaffinarrayに上記mtx00~mtx33までがリストとして格納されているとして処理されています。
affinarray = np.array(affinarray).reshape(4,4,6) dst = cv2.resize(affinarray, dsize=(width, height))
これで画像と同じサイズのアフィン行列の配列が作られます。
このようにして得られたアフィン行列の配列からmapを作成し、remap関数を使って変換します。
X, Y = np.meshgrid(np.arange(w), np.arange(h))
XX = X*dst[:,:,0] + Y*dst[:,:,1] + dst[:,:,2]
YY = X*dst[:,:,3] + Y*dst[:,:,4] + dst[:,:,5]
out = cv2.remap(img1, XX.astype('float32'), YY.astype('float32'), cv2.INTER_CUBIC)
全コードは最後に載せますが、やっていることはこれだけ。エラー処理の類が適当なので、特徴点が少ないエリアを含むようだとうまく行かないかもしれません。パターンマッチングを組み合わせるともっとうまく行くかもしれませんが、ひとまずここまで。
結果として1つのアフィン変換では合いきらなかった2枚の画像が、合うようになりました。異なる行列間のつなぎ目も目立ちません。
ちょっと右上で追い込みが足りません。右上のブロックで対応点取れてない気がします。雲なので特徴点出なかったかな…。エラー処理をもう少し賢くした方がいいかも。

もちろん被写体によるのですが、剛体が相手で手振れ程度の微小変化であれば、それなりに2枚の画像はマッチすると思います。
コード
全コードを載せときます。コード上は16エリアの対応点探索は個別に行わず、画像全体のマッチング結果から各エリアのポイントを切りだしてしています。ちょっと長めですが、関数3つでそれぞれもそんなに長くないのでまぁまぁ。
##
# @file alignment.py
# @date 2020/7/2
# @brief 剛体位置合わせモジュール
import cv2
import numpy as np
##
# @brief AKAZEによる画像特徴量取得
# @param img 特徴量を取得したい画像(BGR順想定)
# @param img 特徴量を取得したい画像(BGR順想定)
# @return apt1 img1に対するkey points
# @return apt2 img2に対するkey points
def get_matcher(img1, img2):
gray1 = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)
gray2 = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)
sift = cv2.AKAZE_create()
# find the keypoints and descriptors with AKAZE
kp1, des1 = sift.detectAndCompute(gray1, None) # query
kp2, des2 = sift.detectAndCompute(gray2, None) # train
if len(kp1) == 0 or len(kp2) == 0:
return None
# Brute-Force Matcher生成
bf = cv2.BFMatcher()
matches = bf.knnMatch(des1, des2, k=2)
# store all the good matches as per Lowe's ratio test.
good = []
for m, n in matches:
if m.distance < 0.7 * n.distance:
good.append(m)
if len(good) == 0:
return None
target_position = []
base_position = []
# x,y座標の取得
for g in good:
target_position.append([kp1[g.queryIdx].pt[0], kp1[g.queryIdx].pt[1]])
base_position.append([kp2[g.trainIdx].pt[0], kp2[g.trainIdx].pt[1]])
apt1 = np.array(target_position)
apt2 = np.array(base_position)
return apt1, apt2
##
# @brief ブロック分割した領域毎の位置合わせ画像生成
# @param img 特徴量を取得したい画像
# @param img 特徴量を取得したい画像
# @param apt1 img1に対するkey points
# @param apt2 img2に対するkey points
# @param BLOCK ブロック分割数
# @return 1mg2に対して位置を合わせたimg1
def get_affine_img(img1, img2, apt1, apt2, BLOCK = 4):
h, w = img1.shape[:2]
w = w//BLOCK
h = h//BLOCK
affinarray = []
for y in range(BLOCK):
for x in range(BLOCK):
sx = x * w
sy = y * h
pt1, pt2 = trim_point([sx, sy], [sx + w, sy + h], apt1, apt2)
if len(pt1) < 8:
pt1 = apt1
pt2 = apt2
tform = cv2.estimateAffinePartial2D(pt2, pt1)[0]
affinarray.append(tform.reshape(6))
h, w = img1.shape[:2]
affinarray = np.array(affinarray).reshape(BLOCK,BLOCK,6)
dst = cv2.resize(affinarray, dsize=(w, h))
X, Y = np.meshgrid(np.arange(w), np.arange(h))
XX = X*dst[:,:,0] + Y*dst[:,:,1] + dst[:,:,2]
YY = X*dst[:,:,3] + Y*dst[:,:,4] + dst[:,:,5]
return cv2.remap(img1, XX.astype('float32'), YY.astype('float32'), cv2.INTER_CUBIC)
##
# @brief 指定された座標の範囲にあるpoint1のマッチングポイント(ペア)を切り出す。
# @param start 切り出したいpoint1の開始座標
# @param end 切り出したいpoint1の終了座標
# @param pt1 切り出したい points1
# @param pt2 切り出したい points2
# @return 切り出されたkey points
def trim_point(start, end, pt1, pt2):
tmp = np.where((start[0] < pt1) & (pt1 < end[0]))
indx = tmp[0][np.where(tmp[1]==0)]
ptx1 = pt1[indx]
ptx2 = pt2[indx]
tmp = np.where((start[1] < ptx1) & (ptx1 < end[1]))
indx = tmp[0][np.where(tmp[1]==1)]
apt1 = ptx1[indx]
apt2 = ptx2[indx]
return apt1, apt2
####################################
## main
if __name__ == '__main__':
img1 = cv2.imread("input1.jpg")
img2 = cv2.imread("input2.jpg")
pt1, pt2 = get_matcher(img1, img2)
img = get_affine_img(img1, img2, pt1, pt2, 4)
cv2.imwrite("output.JPG", img)



コメント