1次の線形回帰をする際に、二乗誤差最小の計算を展開していくとその傾きは分散と共分散でシンプルに表現できることが分かりました。
今回は本当か?というのをPython使って検算してみます。
1次の線形回帰
2次元データ群を直線近似する1次の線形回帰。何ぞ小難しそうな印象を持ちますが、別にさほど難しくなく、二乗誤差を最小にする値を偏微分と連立方程式で解くだけでした。
ゴリゴリと式を展開していくと、えらいシンプルな式に行きつくことを
で確認しました。直線の傾きaは
$$a=\frac{v_{xy}}{v_x}$$
あまりにシンプルなので本当か?と思ってしまいます。
Pythonで検算
そこで今回はPythonのライブラリを使ってその通りの値になるか検算してみます。
使用する関数は、random.multivariate_normalというなんと指定した分散・共分散を持つ乱数を発生させることができるという強力な物です。
こいつを使って発生させた乱数を今度はpolyfitという関数を使って1次近似させた時に正しく計算通りの傾きが出るかを試してみました。
random.multivariate_normal
こいつは多変量正規分布の乱数配列を作ってくれる便利なやつです。APIは色々ありますが、今回は2次元のデータを扱うだけにするので、分かりやすいです。与える変数はメインの3つだけです。
まずは平均値。2つの変数のそれぞれの値を指定します。面倒なので0,0にします。
次に分散と共分散。指定の仕方はいわゆる分散共分散行列の形で渡す用です。ここを適当に振ってみます。
最後に乱数の個数。十分な量がないと近似もうまく行かないだろうと思って1万個くらいでやってみました。
polyfit
これがまた便利な関数。n次の近似をしてくれます。詳細割愛しますが、変数と次数を指定してあげることで傾きと切片を出してくれます。
サンプルコード
今回以前の記事で疑問だったxとyのデータを入れ替えた時の回帰もしてみて、同じ直線にならない事も確認してみます。
import numpy as np
import matplotlib.pyplot as plt
mu = [0,0]
sigma = [[10,15],[15,30]] #分散・共分散行列
x, y = np.random.multivariate_normal(mu, sigma, 10000).T
k = np.polyfit(x, y, 1) #1次近似
l = np.polyfit(y, x, 1) #x,y,入れ替え
xx = np.arange(-20, 20, 1)
yyy = k[0] * xx + k[1] # y = ax + b
xxx = l[0] * xx + l[1] # x = a'y + b'
plt.scatter(x,y)
plt.plot(xx, yyy, color='red')
plt.plot(xxx, xx, color='blue')
plt.show()
恐ろしく短いコードですが、これで
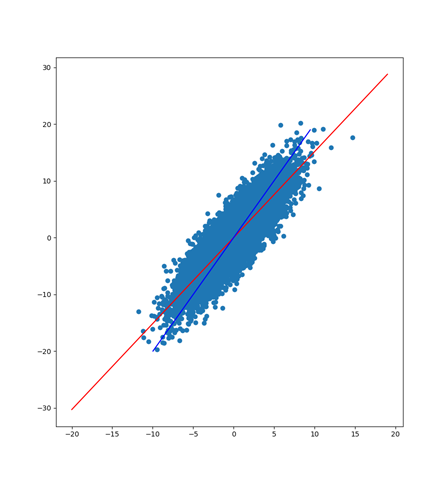
こんなグラフが書けてしまいます。yの誤差を最小にする直線が赤で、xの誤差を最小にする直線が青。全然違う傾きになっています。今回与えた分散・共分散行列は
$$\sum=\left(\begin{array}{c}v_x & v_{xy}\\ v_{xy} & v_y\end{array}\right)=\left(\begin{array}{c}10 & 15\\ 15 & 30\end{array}\right)$$
なので、求まった傾きk[0]は約1.5。確かに共分散15を分散10で割ったものになっています。データを入れ替えると傾きl[0]は0.5。
$$a=\frac{v_{xy}}{v_x}$$
この式通りです。グラフ上は逆数取って2。直線はまるで重なりません。どっちの直線が近いかは微妙。ここまで違うと、意味を理解して使わないと痛い目を見そうです。
分散・共分散の値をあれこれいじると分布が広がったり、すぼまったりする様子もわかります。
計算通り検算終了です。
Cで記述
相関係数算出の式
double soukankeisu(point* src,int cnt){
double avex = 0.0;
double avey = 0.0;
for(int i=0;i<cnt;i++){
avex += src[i].x;
avey += src[i].y;
}
avex = avex/cnt;
avey = avey/cnt;
double kyobunsan = 0.0;
double hensax = 0.0;
double hensay = 0.0;
for(int i=0;i<cnt;i++){
kyobunsan += (src[i].x - avex) * (src[i].y - avey);
hensax += (src[i].x - avex) * (src[i].x - avex);
hensay += (src[i].y - avey) * (src[i].y - avey);
}
return (kyoubunsan*kyoubunsan) / (hensax*hensay);
}
まとめ
線形回帰の答えもシンプルなら、Pythonのコードも恐ろしくシンプルです。乱数生成時に任意の分散・共分散を入れられるというのがとんでもないなと思ってしまうのですが、絶対あり得ない行列だってあるはずです。例えば分散0なのに共分散値を持ったりすることはないはず。そんな場合は必ずしもうまく行かないはずです。
今度はどうやってこんな正規乱数作っているかが気になり始めました。


コメント