ある任意の分散共分散を持つ乱数の生成に関して少し考えてみます。今回も計算に行列の計算を使います。検算にPythonを使います。
分散共分散はその分布を特徴づける重要な値です。これをコントロールできると色々便利。だと思う。
ある分布を持つデータ群から、その分布の分散共分散を求めることで、近似直線が引ける事を以前計算してみました。いわゆる最小二乗法による線形回帰です。
逆にある直線に近似できるような分布はその直線の式から求められるということにもなりそうです。
今回は任意の分散共分散を持つ多次元の乱数を作る方法について考えてみます。計算が分かりやすい様に2次元で記述しますが、N次元でも計算は同じです。行列すげー。
結論から言うと、1次元の正規乱数列を複数用意し、任意の分散共分散行列から変形した行列を乗じることで簡単に求まってしまいます。以下解き方です。
正規乱数
任意の分散と平均を持つ1次元の正規乱数(ガウス分布)は何らかの手段で作れているものとして仮定します。平均0、分散1の乱数とします。
分布(ヒストグラム)としてはよく見るこんな形です。
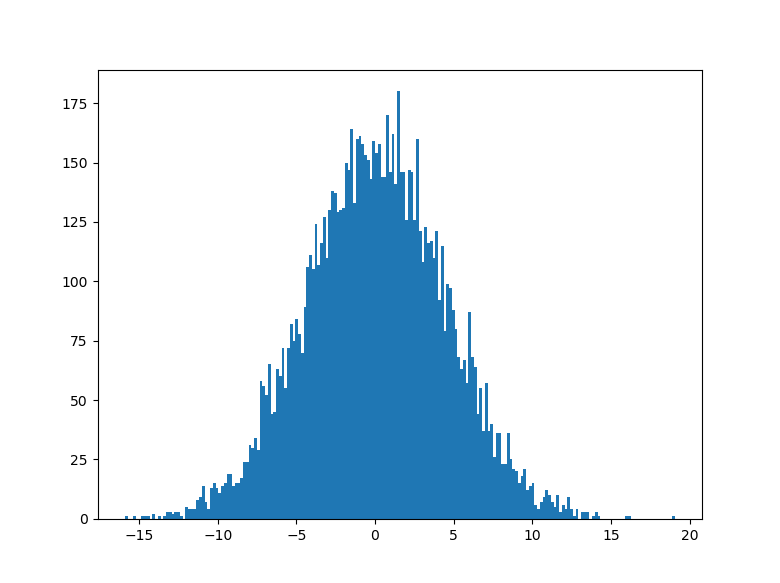
このような乱数列を2つ用意します。
2つの乱数\(r_1\)と\(r_2\)を行列で表現すると、
$$r=\left(\begin{array}{c}r_{11} & r_{12} & .. & r_{1n}\\ r_{21} & r_{22} & .. & r_{2n}\end{array}\right)$$
こんな感じ。
分散共分散行列
分散共分散行列とは、2つのデータx,yそれぞれの分散を対角に、共分散が周りに来るような行列でその分布の特徴を示します。定義としてはこんな感じ。
$$\sum=\left(\begin{array}{c}v_x & v_{xy}\\ v_{xy} & v_y\end{array}\right)$$
このように分散共分散行列は通常対称行列になります。分散、共分散の定義は平均を\(\mu\)とすると、シグマを使って
$$v_x=\frac{1}{N}\sum_{i=1}^N(x_i-\mu_x)^2$$
$$v_{xy}=\frac{1}{N}\sum_{i=1}^{N}(x_i-\mu_x)(y_i-\mu_y)$$
です。
上記の分布\(r\)の分散共分散行列は、それぞれの乱数の平均は0、分散は1とし、互いに独立なので共分散は0(無相関)、すなわち単位行列になります。
行列で表現すると、この乱数列\(r\)とその転置行列の積で表現することができます。
$$\sum=rr^{\top}=\left(\begin{array}{c}v_{r_1} & v_{r_1r_2}\\ v_{r_1r_2} & v_{r_2}\end{array}\right)=\left(\begin{array}{c}1 & 0\\ 0 & 1\end{array}\right)=I$$
この式を展開すればまぁ分かりますね。それぞれの要素を乗じて和を取っているのでそれほど違和感はありません。分散共分散行列の定義通りです。
前述の通り分散共分散行列は通常対称行列です。対称行列同士の積もまた対称行列になります。また対称行列は転置しても中身が変化しません。(ちょっと手計算すればすぐ分かります。)
そこでとある対称行列\(A\)を上記の乱数列\(r\)に乗じた新たな乱数列\(Ar\)を考えると、その分散共分散行列は、
$$\sum=Ar(Ar)^{\top}=Arr^{\top}A^{\top}=AA^{\top}=A^2$$
となり、\(A^2\)になります。しれっと計算しましたが、2つの行列の積の転置は、それぞれの行列の転置の順序を逆にした積と一致するという性質と、対称行列の転置は対称行列と同じという性質を使って計算してます。
ある対称行列\(A\)を独立な平均0、分散1の正規乱数列\(r\)に乗じた時の分散共分散行列は\(A^2\)となる。ということが分かります。\(A^2\)の平方根を求められれば任意の分散共分散を持つ乱数が作れそうです。
固有値分解
次はその平方根の求め方です。これには固有値分解を用います。この詳細は割愛しますが、特に対称行列の固有値分解はシンプルで逆行列を求める必要がないのが素敵です。
ある対称行列\(B\)を固有値分解するとその固有値、固有値ベクトルはこのように表現できます。
$$B=V\Lambda V^{\top}=V\Lambda V^{-1}$$
この\(B\)の平方根を求めます。真ん中の\(\Lambda\)は対角行列(定義)になっているので、\(B\)の平方根は\(\Lambda\)それぞれの値の√を取るだけです。そのようにしてこの式を分解してみると、
$$B=V\Lambda V^{-1}=V\sqrt{\Lambda}\sqrt{\Lambda} V^{-1}=V\sqrt{\Lambda}V^{-1}V\sqrt{\Lambda} V^{-1}$$
となり、めでたく
$$\sqrt{B}=V\sqrt{\Lambda} V^{-1}=A$$
と求まります。つまり、任意の分散共分散行列\(B\)を持つ乱数は、その固有値分解した値の平方根を取った新しい行列\(A\)を正規乱数列に乗じる事で求まる。ということが示せました。平均値\(\mu\)はただのオフセットなので最終的には、
$$r’=Ar+\mu$$
これで任意の分散共分散\(B\)の値を持つ平均\(\mu\)の分布は、互いに独立な平均0、分散1の分布\(r\)に上記計算で求まる\(A\)を乗じる事で求められる事が分かりました。
あまりこの答えにたどり着いている計算を紹介しているサイトが探し出せませんでしたが、多分合ってると思います。多分。
検算
式の上では合っている様に見えます。なのでPythonで検算してみます。
比較対象はrandom.multivariate_normal関数です。こいつが任意の分散共分散行列から乱数発生させてくれるので、それと今回の計算結果を比較します。
コード
import numpy as np import matplotlib.pyplot as plt import scipy.linalg mu = [0,0] sigma = [[20, 5], [5, 10]] # 分散・共分散行列 # ライブラリで乱数生成 x, y = np.random.multivariate_normal(mu, sigma, 10000).T # sigmaの平方根の計算 L, V = np.linalg.eig(sigma) # 固有値・固有ベクトル rL = np.diag(np.sqrt(L)) # 固有値のルートを対角行列へ A = np.dot(V, np.dot(rL, V.T)) # Aが正しくsimgaのルートになっているか検算 AA = scipy.linalg.sqrtm(sigma) # 行列のルート # A == AA # 平均0,分散1の正規乱数をかけるて平均値を足す。 x2, y2 = np.dot(A, np.random.randn(2, 10000)) x2 = x2 + mu[0] y2 = y2 + mu[1] k = np.polyfit(x, y, 1) # ライブラリの乱数の1次近似 k2 = np.polyfit(x2, y2, 1) # 自分で計算した乱数の1次近似 xx = np.arange(-20, 20, 1) yy = k[0] * xx + k[1] # 直線の式 y = ax + b yy2 = k2[0] * xx + k2[1] plt.scatter(x, y) plt.scatter(x2, y2) plt.plot(xx, yy, color='red') plt.plot(xx, yy2, color='blue') plt.show()
解説
10000個の乱数で比較します。リファレンスとする乱数は, y = np.random.multivariate_normal(mu, sigma, 10000).Tで作ります。sigmaが分散共分散行列。
L, V = np.linalg.eig(sigma) # 固有値・固有ベクトル
に相当する式が、
$$B=V\Lambda V^{\top}=V\Lambda V^{-1}$$
これ。ちなみにVをひっくり返したような記号はΛ(Lambda、ラムダ)です。固有値λの大文字です。なので変数L。
rL = np.diag(np.sqrt(L)) # 固有値のルートを対角行列へ
ここで固有値Λのルートを取って、対角行列(diag関数を使用)にしています。これがrL。
A = np.dot(V, np.dot(rL, V.T))
これでsigmaのルートを取った行列Aが完成します。式で表現すると、
$$A=V\sqrt{\Lambda} V^{\top}$$
この計算結果が正しいかどうかをscipyの関数(scipy.linalg.sqrtm(sigma))を使って検算しています。一致しました。
続いて正規乱数を二つ用意(np.random.randn(2, 10000))して、先に作った行列Aと掛け算します。その結果に平均値muを加算して完成です。
このようにしてできた乱数列x2,y2がリファレンスのx,yと近い分布を持っているかどうかをプロットして確認します。
その前にこの2つの分布の線形回帰をして直線を求めておきます。この直線が同じであれば作られた2つの乱数はほぼ同じものと解釈できます。この直線も一緒にプロットします。結果
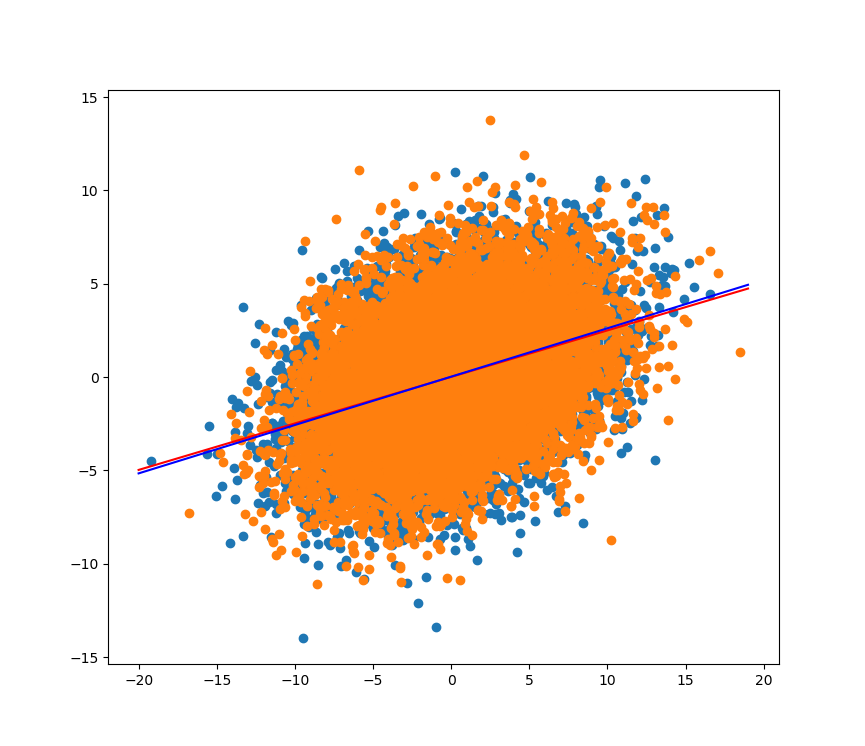
まぁ似たような分布が2色でて、似たような直線が2本引けているので、あってるのではなかろうかと思われます。sigmaやmuをいじっても似た傾向なので計算は合ってそうです。
まとめ
頑張って任意の分散共分散を持つ乱数列を発生させるメカニズムを解いてみました。欲しい分散共分散行列のルートを取るだけですが。Pythonの検算からも多分あってると思います。なんとなくわかった気になります。

コメント