Harrisのコーナー検出を魂で理解する

　ハリスのコーナー検出。画像処理で特徴点を探し出す基本となる処理です。OpenCVのチュートリアルではだいぶ説明がはしょられています。さすがにあれでは分かりません。調べれば調べるほど泥沼にはまっていったのでその経緯をまとめて、数学が分からない人間でも直感で分かるように紐解いていきます。

定義式を理解する
テーラー展開
行列の対角化
画像で考える
まとめ

定義式を理解する

　まずは基本の式です。この式そのものはそれほど難しくはありません。

$$E(u,v)=\sum_{x,y}w(x,y)\left[I(x+u,y+v)-I(x,y)\right]^2$$

　ちょっと$(u,v)$だけずらした位置との画素値の差分を取って、その大きさを計算してみよう。それが大きなところがコーナーだ。と言っている式です。

　図を使って考えます。横エッジ、縦エッジ、フラット、コーナーをそれぞれ縦横にずらしたもので考えてみます。

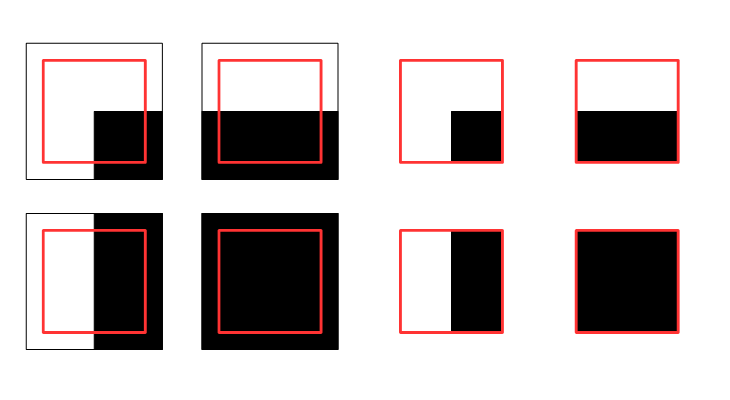
　まずは横にずらしてみます。

　横エッジの画像では差分はありません。フラットは言わずもがな。縦エッジとコーナーの画像では差分が多く出ます。

　今度は縦にずらしてみます。

　今度は縦エッジの画像での差分は小さく、横とコーナーの画像では差分が多く出ます。フラットは…まぁいいか。

　このように$u,v$をどの方向に動かしても差分が大きく出る位置それがコーナーだ。というのがこの式の定義です。まぁそれなりに意味は分かりますね。

　ここまでの説明は色々なサイトでもされているので理解はできます。

テーラー展開

　次に引っかかるのがテーラー展開。この定義式をテーラー展開するそうです。テーラー展開に関しては細かく突っ込みませんが、とある関数をある値aの近傍で多項式近似する便利な展開です。

　このテーラー展開を1次の項で打ち切って、式を展開しています。

　テーラー展開を1次で打ち切るとはどういうことか？定義の式から見てみると、

$$f(x)\approx f(a)+f'(a)(x-a)$$

　こんな感じです。まぁ雑な近似ですがそこそこいい感じで値を近似します。実際適当な関数を例に、この式が何を示しているか考えます。

　$f(x) = x^2$とします。$x = 1.017$の時の$x^2$を求めよ。みたいな事を考えてみます。そんなの$x$はほぼ1だから2乗しても1でしょ。ってのが$a = 1.0$ でテーラー展開をして0次で打ち切った時の答えになります。

$$f(1.017)=f(1)=1^2=1$$

　それじゃあまりにもってんで、1次の項、$f'(x) = 2x$を使って、近似したのが1次のテーラー展開の結果。

$$f(1.017)=f(1)+2f'(1)*0.017=1^2+2*0.017=1.034$$

　実際の答えは1.034289なのでまぁいい感じに近い数字になってます。

　$a$の近傍ではそれなりにいい感じの近似をしてくれるので、先の$(u,v)$が十分小さければこの展開を1次で打ち切ってもそこそこいい感じに近似ができるだろう。ってのがこの式の展開の意味です。

　先のテーラー展開の式を$a=x,x=x+u$で置き換えると（xの周りでテーラー展開すると）、

$$f(x+u)\approx f(x)+f'(x)u$$

　こんな式になります。さっきの2乗の式でいうところの$x$が1.000で、$u$が0.017って所です。

　変数が2つでも同じで、

$$f(x,y)=f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b)$$

　同じように変形して

$$f(x+u,y+v)=f(x,y)+f_x(x,y)u+f_y(x,y)v$$

　こんな感じに置き換えられるので、ハリスの定義式は

$$E(u,v)=\sum_{x,y}w(x,y)\left[I(x+u,y+v)-I(x,y)\right]^2 \\
=\sum_{x,y}w(x,y)\left[I(x,y)+uI_x(x,y)+vI_y(x,y)-I(x,y)\right]^2\\
=\sum_{x,y}w(x,y)\left[uI_x(x,y)+vI_y(x,y)\right]^2\\
=\sum_{x,y}w(x,y)\left[u^2I_x^2(x,y)+2uvI_x(x,y)I_y(x,y)+v^2I^2_y(x,y)\right]$$

　式が長いのでひとまず以下のように置き換え

$$\sum_{x,y}w(x,y)I_x^2(x,y)=I^2_x\\
\sum_{x,y}w(x,y)I_y^2(x,y)=I^2_y$$

　この式が意味しているのは、微分した画像に窓関数(w)を畳みこんでいるって事ですね。

$$E(u,v)=u^2I^2_x+2uvI_xI_y+v^2I^2_y$$

　こんな感じに展開出来てしまいます。かなりシンプルな式になります。

　2×2の行列を使って、

$$E(u,v)=\begin{bmatrix}u & v \end{bmatrix}\begin{bmatrix}I^2_x & I_xI_y \\ I_xI_y & I^2_y \end{bmatrix}\begin{bmatrix}u \\ v \end{bmatrix}=a^\top Ma$$

　こんな感じに展開出来てしまいます。色々なサイトでよく見る式が完成します。

行列の対角化

　次からがややこしい。この行列の固有値、固有ベクトルが突然登場します。まずここで理解放棄してしまいそうになるのですが、もうひと踏ん張りです。

　この2×2行列Mはいわゆる対称行列ってのになっています。対称行列でググれば色々解説が出てくると思いますが、こいつはかなり便利な奴で、

　必ず実数で固有値が得られる。（対角化できる）

　固有ベクトルは直交する。（正規直交基底）

　となるようです。（詳しくは「正規直交基底」とか「対角化」とかでググってください。）なのでMは対角化できることが保証され、先の式は対角化することで、

$$E(u,v)=a^\top Ma=a^\top P^\top APa=(Pa)^\top A (Pa)$$

　こんな式になります。このPがポイント。先の定理より固有ベクトルは直交して長さが1のベクトルなので図で示すと

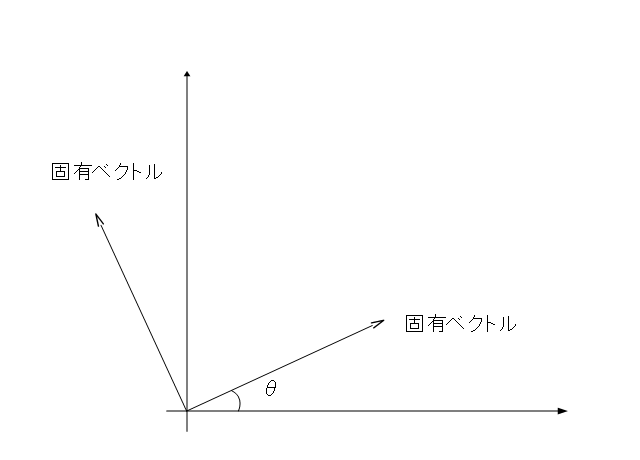
　こんな2本のベクトルになっているはず。この2本のベクトルを並べたPはなす角θを使って

$$P=\left(\begin{array}{c}\cos\theta & \cos(\theta+90) \\ \sin\theta & \sin(\theta+90)\end{array}\right) = \left(\begin{array}{c}\cos\theta & -\sin\theta \\ \sin\theta & \cos\theta\end{array}\right)= \left(\begin{array}{c}\cos(-\theta) & \sin(-\theta) \\ -\sin(-\theta) & \cos(-\theta)\end{array}\right)$$

　こんな感じで変換できそうです。この式見覚えがあります。そうアフィン変換の回転を意味する式です。この行列が$(u,v)$に引っ付いているので、$(u,v)$を回転させた軸で同じ計算をしている事になります。

　ある軸$(x,y)$で$(u,v)$だけちょっと動かすと、それぞれθで回転した軸で$(u,v)$だけちょっと動かしたのと等価になるよ。とこの式は言っています。なぁんかこの辺り狐につままれた感じがしますが、意味合いはそのはずです。

　式は完成しました。新しい軸で、$(u,v)$だけ動かしたときにこの値が大きくなるような行列Aを持つ箇所がコーナーである。と言っています。

　$u$方向にも$v$方向にもどちらの方向に動かしても大きな値を取るにはその対角成分（すなわち固有値）がいずれも大きい値を取る必要があります。これがすなわちOpenCVのチュートリアルで見るこの図

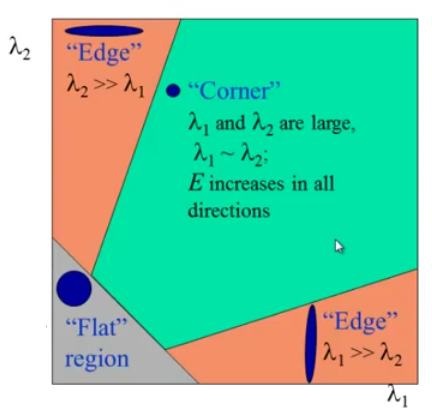
　これが意味する事になります。分かったような分からないような。

　各画素の固有値を求めるには計算コストが半端ないので、これをいい感じに丸めた式で2つの固有値が両方とも大きい値を出す所を見つけるのがハリスさんの

$$R=det(M)-k(trace(M))^2=(\lambda_1\lambda_2)-k(\lambda_1+\lambda_2)^2$$

　この式。$k$の値は経験的に求めるそうで、0.04～0.15あたりがおすすめだそうです。なるほど。

画像で考える

　ここからはPython使って処理を手書きしながら画像を見ていきます。

　先の対角化する前の式に登場した$I_x,I_y$の意味を考えます。これは微分画像、Sobelフィルタを適用した画像になります。こんな画像を入力として考えると、

　その微分画像の2乗$I^2_x,I^2_y,I_xI_y$はそれぞれ

img = cv2.imread("corner.png")
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
gray = np.float32(gray)

Ixx = gray[1:-1, :-2] - gray[1:-1, 2:]  # x方向の微分
Iyy = gray[:-2, 1:-1] - gray[2:, 1:-1]  # y方向の微分

Ixy = Ixx * Iyy  # 右の画像
Ixx = Ixx * Ixx  # 左の画像
Iyy = Iyy * Iyy  # 中央の画像

　こんな感じの画像になります（$I_xI_y$は符号付き）

　それに対して窓関数（通常はガウス関数だそうです）を畳みこむので、結果としては先の画像がボケた感じになります。

Ixx = cv2.GaussianBlur(Ixx, (5, 5), 0)
Iyy = cv2.GaussianBlur(Iyy, (5, 5), 0)
Ixy = cv2.GaussianBlur(Ixy, (5, 5), 0)

　この3つの画像の各画素が行列Mを構成します。

　これをやはり横エッジ、縦エッジ、コーナー、フラットで考えると横エッジでは$I_x$の値が0なので、行列は右下を除いてすべて0。

$$ \left(\begin{array}{c}0 & 0\\ 0 & I_y^2\end{array}\right) $$

　縦エッジでは$I_y$が0なので、行列は左上を除いてすべて0。

$$ \left(\begin{array}{c}I_x^2 & 0\\ 0 & 0\end{array}\right) $$

　フラットは全部0。コーナーでは横エッジにパワーがあるところでは縦エッジのパワーが0。縦エッジにパワーがあるところでは横エッジのパワーが0なので、結果として対角行列になります。

$$ \left(\begin{array}{c}I_x^2 & 0\\ 0 & I_y^2\end{array}\right) $$

　行列Mが対角行列に近くその対角成分がそこそこ大きい。これがコーナー候補の場所になります。ただしコーナーは何も縦横にまっすぐとは限らず、回転していることも考えられます。

　このサンプルだとここは45°回転してます。

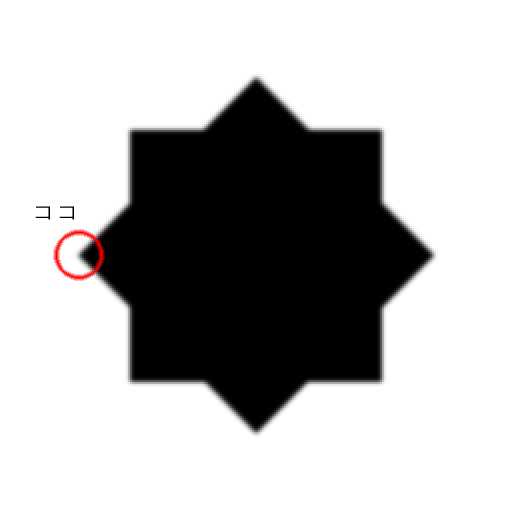
　それが先の対角化を行う真意なのかなと解釈しています。無理やり対角行列になる回転軸を考えて、そこでその対角成分の大小を考えることでコーナーらしさを導き出す。そんな所かなと。

　くそ真面目に全画素の固有値を求めて、2つの固有値の小さい方だけを選んで画像にしてみると見事にコーナーが検出されています。

h, w = Ixx.shape
M = np.array([[0.0, 0.0], [0.0, 0.0]])

for y in range(h):
    for x in range(w):
        M[0, 0] = Ixx[y, x]
        M[0, 1] = Ixy[y, x]
        M[1, 0] = Ixy[y, x]
        M[1, 1] = Iyy[y, x]

        s = np.linalg.eigvals(M) # 固有値分解
        if s[0] > s[1]: # 小さい方をIyyへ（大きい方をIxxへ）
            Ixx[y, x] = s[0]
            Iyy[y, x] = s[1]
        else:
            Ixx[y, x] = s[1]
            Iyy[y, x] = s[0]