360度カメラ、全天球画像の変換　グルグルまわしてみる

　360度カメラで撮影した写真を変換してグルグルまわしてやろうと思います。

　前回の記事でまずは円に投影することを試してみましたが、今回はその結果を使って緯度、経度にグルグルまわして見ようと思います。

　いろいろなサイトでややこしい計算結果の式だけ載っているものは見かけるのですが、その意味がよくわからないのでそこを紐解きます。

　ちなみにいわゆるパノラマっぽい任意視点の画像変換に関しては別記事でもう少し本格的に試しています。思ったのと違うと思った方はこちらも見てみてください。

正距円筒図法
円への投影
グルグルまわす
3次元座標へのマッピング
3次元座標の回転
Pythonで記述
まとめ

正距円筒図法

　前回の復習。

　360度カメラで撮影された画像は、カメラを中心としてぐるっと1周分が1：2の縦横比の画像として記録されています。このフォーマットはいわゆる世界地図と同じように、縦に緯度、横に経度で示した形式になっています。緯度、経度の同じ角度が等間隔になるようにレイアウトされるため、左右に360度、上下に180度、1:2の画像フォーマットになります。全天球画像とかエクイレクタングラー(equirectangular)とか調べるといろいろ出てきます。

　緯度経度は地球の中心から赤道を向いて、ぐるっと一周する向きが経度、見上げる見下げる角度が緯度になります。

　ただ今回の記事では説明を簡単にするために経度方向は180度分の正方形の画像で考えます。

円への投影

　詳細は前回の記事を参照。赤道を正面に見た形での投影は比較的簡単に計算できます。

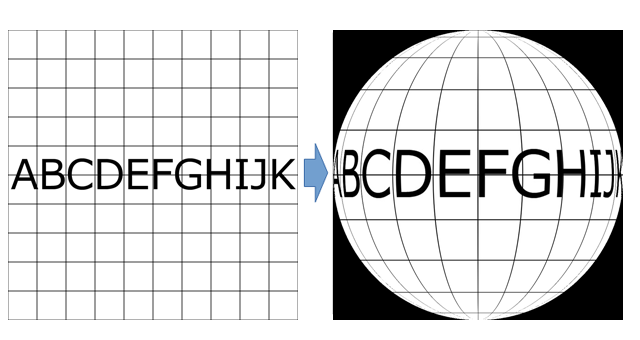
グルグルまわす

　この投影を赤道を正面にするのではなく、任意の緯度・経度を正面にした視点へ変換することを考えます。その結果地球がグルグル回るように視点を変えることができるはずです。

　経度（横方向）の回転、いわゆる自転は比較的簡単に実現できます。入力の画像を横方向にシフトしてやるだけでできちゃいます。

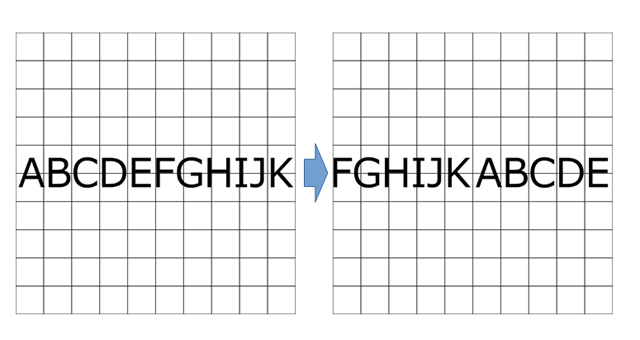
　これで経度の方向へ90度回ったことになります。グリニッジ天文台を中心にした世界地図を日本を中心にした世界地図にずらしたようなイメージです。

　緯度（縦方向）の回転はちょっと難しいです。いろいろ図を書いてどのように投影されるか考えたのですが、いまいちわかりやすいシンプルな方法が思いつかなかったので、あきらめて3次元で考えることにします。

　緯度φ、経度θで表現される地図は地球という３次元の球体に一意にマッピングできます。その３次元座標x,y,zを回転させることで新しい地図を作ります。そうすることで緯度・経度の回転を実現させます。

3次元座標へのマッピング

　緯度φ、経度θの座標が3次元の球体のどこへマッピングされるか考えてみます。

　球の中心を原点に緯度方向にz軸をとり、経度ゼロ（グリニッジ天文台の経度）をx軸ととると、この図のように任意の点はθとφで特定できる気がします。

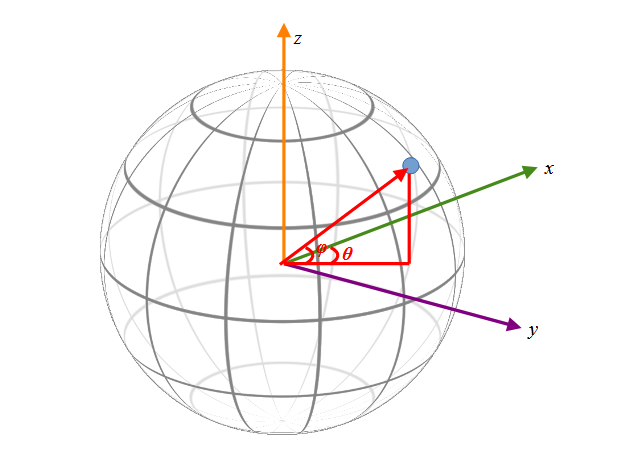
　この図をまずはy-z平面へ投影（地球を横から投影）した時のzの値を考えてみます。

　すると半径rの球はz=rsinφへ投影されます。図はちょっと正確ではないです。θ=0の時を例にした図だと思ってください。θが値を持つ場合必ずしもy=rcosφではないですが、zはどんなθでもz=rsinφです。

　次にx-y平面に投影（地球を真上から投影）した時のx,yの値を考えてみます。

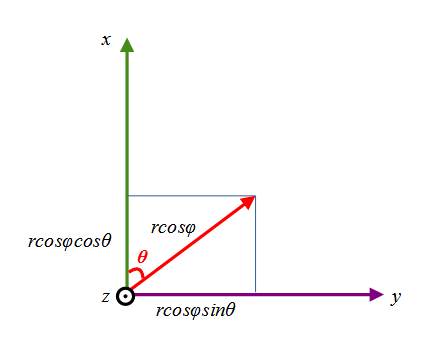
　すると投影される長さはrcosφになるので、任意の緯度経度φ、θは、球の中心を原点としたx,y,z座標

$$ x = r\cos\phi\cos\theta \\
y = r\cos\phi\sin\theta \\
z = r\sin\phi$$

　にマッピングされることがわかります。

　前回の記事では、結果としてz-y平面への投影をしていたことになりますね。

3次元座標の回転

　この座標の3次元座標上での回転を考えます。経度方向は先に書いたように地図を横にずらせば良いだけなので、緯度方向にまわしてみます。

　こんな感じ。

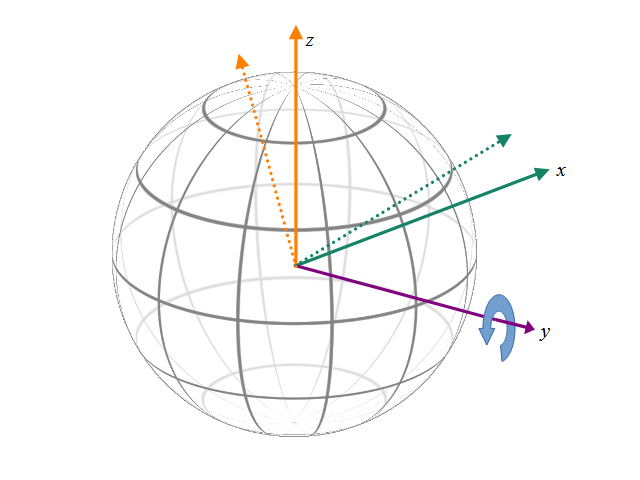
　つまりy軸を回転軸にすれば良いことになります。

　つまりx-z平面での回転のアフィン変換を行えば良いことになります。y軸回転なのでyの値は変化しません。

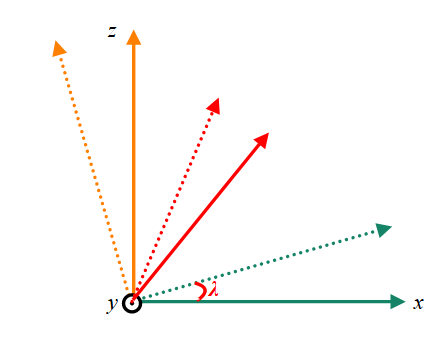
　3次元の回転というのは、Wikipediaによると一般的にローリングとかいわれるみたいでこのy軸の回転はピッチとなるようです。

　y軸変化のないx-zの回転なので、2次元のアフィン変換と同じように回転成分λだけ回転させようと思ったら、

$$ \left(\begin{array}{c}\cos\lambda & 0 & \sin\lambda \\ 0 & 1 & 0 \\ -\sin\lambda & 0 & \cos\lambda\end{array}\right) \left(\begin{array}{c}x\\ y \\ z\end{array}\right)$$

　こんな行列を乗じれば良いです。2次元の回転行列と同じです。yの値は変化しません。先に得られたx,y,zに対してこの行列を乗じることで、このx,y,z座標を回転させることが可能になります。

　このようにして回転させた新しい座標をz-y平面に投影させることで、球として正面から見た画像に変換されます。それをグルグル回します。

Pythonで記述

　Pythonで記述してみます。とあるπ/16だけずらしたサンプルです。

import cv2
import numpy as np

img = cv2.imread("src.jpg")

h,w = img.shape[:2]

w = w//2
h = h//2
r = h

X, Y = np.meshgrid(np.arange(-w,w), np.arange(-h,h))

phi = np.arcsin(Y/r)
theta = np.arcsin(X / (r * np.cos(phi)))

x = np.cos(phi)*np.cos(theta)
y = np.cos(phi)*np.sin(theta)
z = np.sin(phi)

rot = np.pi/16
    
xx = x*np.cos(rot) + z*np.sin(rot)
yy = y
zz = -x*np.sin(rot) + z*np.cos(rot)
    
phi = np.arcsin(zz)
theta = np.arcsin(yy / np.cos(phi))
    
Y = (2 * phi / np.pi) * h + h
X = (2 * theta / np.pi) * w + w
    
out = cv2.remap(img, X.astype(np.float32), Y.astype(np.float32), cv2.INTER_LINEAR)
cv2.imwrite("dst.jpg", out)

　前回のコードにちょいと足すだけで実現できます。meshgridやremapの使い方が初めて見るととっつきにくいかもしれませんが、それ以外は上で示した計算式通りです。このコード上xxの計算は不要なのですが、行列をかけてることを示すためにひとまずつけておきます。

　画像座標(x,y)→緯度経度(φ,θ)→(x,y,z)→回転(xx,yy,zz)→緯度経度（φ、θ）→画像座標(X,Y)の順で変換しています。

　前回の画像をサンプルにします。

　無回転の

　こいつをπ/16だけずらした画像は

　角度に対してfor文でループさせるとグルグルと回ったパラパラ漫画ができます。

　適当な写真で試すと

　こんな感じ。

　変換を一部はしょったコードで任意の緯度を正面にした新たな地図（全天球画像）が作れます。

#X, Y = np.meshgrid(np.arange(-w,w), np.arange(-h,h))

#phi = np.arcsin(Y/r)
#theta = np.arcsin(X / (r * np.cos(phi)))

theta, phi = np.meshgrid(np.arange(-np.pi/2, np.pi/2, np.pi/w),np.arange(-np.pi/2, np.pi/2, np.pi/h))

　日本を赤道に持ってきたような世界地図もこんな計算で作れます。緯度方向の回転成分を変化させた全天球画像もこの計算で作れます。

　ちなみに経度方向にグルグルまわそうと思ったらz軸を回転軸にした回転（ヨー）なので、行列式は

　$$ \left(\begin{array}{c}\cos\lambda & \sin\lambda & 0 \\ -\sin\lambda & \cos\lambda & 0 \\ 0 & 0 & 1 \end{array}\right) \left(\begin{array}{c}x\\ y \\ z\end{array}\right)$$

　こんな感じで一部コードを

#ピッチ
#xx = x*np.cos(rot) + z*np.sin(rot)
#yy = y
#zz = -x*np.sin(rot) + z*np.cos(rot)

#ヨー
xx = x*np.cos(rot) + y*np.sin(rot)
yy = -x*np.sin(rot) + y*np.cos(rot)
zz = z

　このように書き換えれば横方向のグルグルも簡単に試せます。この回転行列の積をとって乗じれば2軸の回転ができます。