360度カメラの全天球画像ビューアーを作る　その１

　360度カメラで撮影した写真を任意の視点からの画像（パノラマ画像）へ変換するビューアーを作ってみようと思います。結果3回シリーズになりました。その1回目です。目次としてはこんな感じ。

　1.360度写真の平面投影
　2.視点の変更と背面の投影
　3.視点の回転

　まずは平面投影をしてみます。ちょっと前の記事で円へ投影する計算はしてみたのですが、いわゆるビューアーとはならなかったので、もう少し真面目に計算します。

　THETAという360度カメラがあります。このカメラに付属するビューアーを目標に作ってみます。ちなみにTHETAを持っていなくてもダウンロードできるのでほかの360度カメラの写真も眺めることができます。ちなみにこのビューアーは入力画像の縦横の比率が１：２であればなんでも開けます。

　これを真似します。基本の仕組みを考えてみます。

360度写真（正距円筒図法）
3次元座標へのマッピング
視点の定義
撮像面の定義
投影
Pythonで記述
結果
まとめと今後

360度写真（正距円筒図法）

　360度カメラで撮影された画像は、カメラを中心としてぐるっと1周分が1：2の縦横比の画像として記録されています。このフォーマットはいわゆる世界地図と同じように、縦に緯度、横に経度で示した形式になっています。緯度、経度の同じ角度が等間隔になるようにレイアウトされるため、左右に360度、上下に180度、結果として1:2の画像フォーマットになります。

　緯度経度は地球の中心から赤道を向いて、ぐるっと一周する向きが経度、見上げる見下げる角度が緯度になります。いわゆる世界地図ですね。エクイレクタングラー(equirectangular)とかそんな呼び方するようです。

3次元座標へのマッピング

　前記画像が世界地図なら、地球面へマッピングできるはずです。任意の緯度φ、経度θの座標が3次元の球体のどこへマッピングされるか考えてみます。

　球の中心を原点に緯度方向にz軸をとり、経度ゼロ（グリニッジ天文台の経度）をx軸ととると、この図のように任意の点はθとφで特定できる気がします。

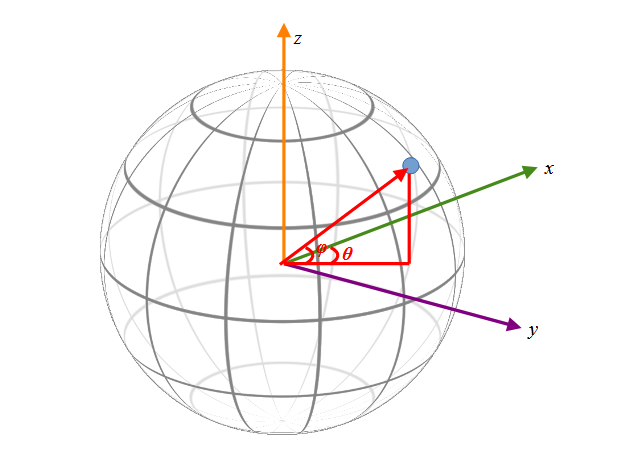
　この図をまずはy-z平面へ投影（地球を横から投影）した時のzの値を考えてみます。

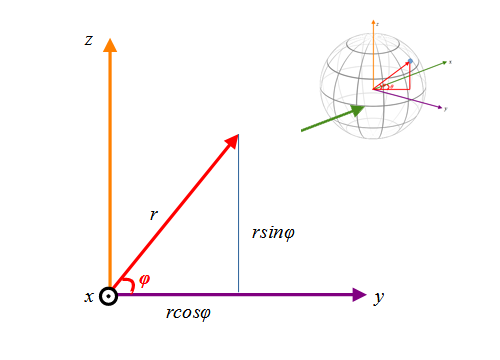
　すると半径rの球はz=rsinφへ投影されます。図はちょっと正確ではないです。θ=0の時を例にした図だと思ってください。θが値を持つ場合必ずしもy=rcosφではないですが、zはどんなθでもz=rsinφです。

　次にx-y平面に投影（地球を真上から投影）した時のx,yの値を考えてみます。

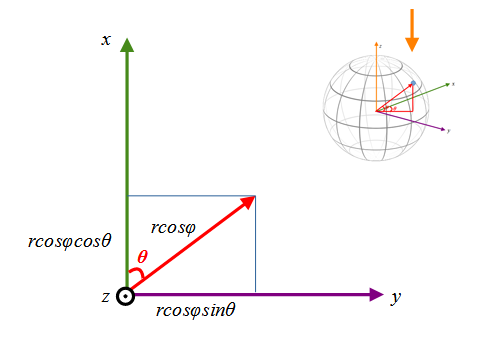
　すると投影される長さはrcosφになるので、任意の緯度経度φ、θは、球の中心を原点としたx,y,z座標

$$ x = r\cos\phi\cos\theta \\
y = r\cos\phi\sin\theta \\
z = r\sin\phi$$

　にマッピングされることがわかります。半径を１とするとその球面上の任意のx,y,zから、φ、θは

$$ \phi = \arcsin (z) \\
\theta = \arcsin ( \frac{y}{\cos \phi}) $$

　と求まります。（x不要ですね）

視点の定義

　360度写真が3次元の点にマッピングできることがわかりました。そこでこの3次元の点を、ある視点からの2次元平面の座標に再マッピングすることを考えます。

　球体の内側から球の表面の写真を撮るイメージ。こんな感じ

　今回視点はx軸上のある点と定義します。このx座標を$x_1$とします。これが視点です。

　ここを視点に図中の青い長方形の2次元へのマッピングを考えます。

撮像面の定義

　球の半径は1に正規化して計算することにします。

　視点から像を結ぶ青い長方形を、撮像面（センサ面）と呼ぶことにします。撮像面の中心をx軸が垂直に通るように定義し、その幅は$2w$、高さ$2h$の長方形とします。

　この撮像面のx座標を$x_2$とします。この$x_2$は視点$x_1$より大きい値（前）である必要があります。

　z=0でxy平面の輪切りをするとこんな感じになります。

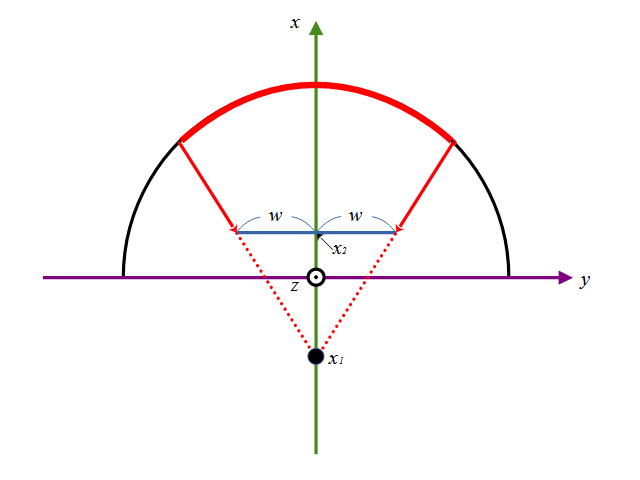
　赤の曲線で示した範囲が撮像面に投影されることになります。

投影

　撮像面の任意の座標$(ww,hh)$に球のどこのxyz座標が投影されるか計算します。撮像面$(ww,hh)$座標の3次元の座標は$(x_2,ww,hh)$になります。

　視点位置から$ww,hh$を通る直線の式を考えます。xy平面で考えると図のような直線$y=a_1 x + b_1$になります。

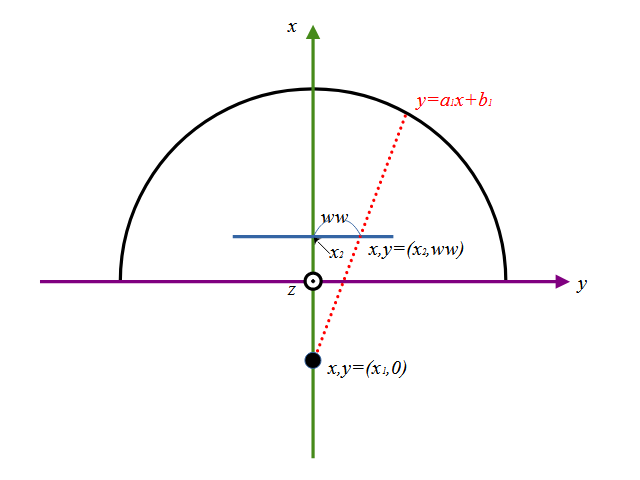
　この直線は既知の2点、視点と撮像面$x,y =(x_1,0)(x_2,ww)$を通るので、$a_1,b_1$はそれぞれ

$$ a_1 = \frac{ww}{x_2 – x_1} \\
b_1 = -a_1 x_1 $$

　となります。

　同じようにxz平面で考えてみます。

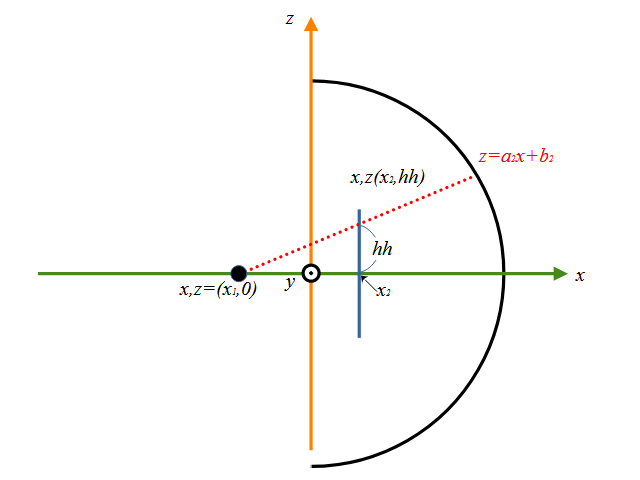
　同様に直線を$z=a_2 x + b_2$とし、2点$x,z = (x_1,0)(x_2,hh)$を通るので、\(a_2,b_2)\はそれぞれ

$$ a_2 = \frac{hh}{x_2 – x_1} \\
b_2= -a_2 x_1 $$

　となります。

　この直線と球の交点を考えます。この球の半径は1とおいているので式は

$$ x^2+y^2+z^2=1 $$

　なので、先に求めた$a_1,a_2,b_1,b_2$を使って

$$ x^2+(a_1 x+b_1)^2+(a_2 x+b_2)^2=1 \\
x^2 + a_1 ^2x^2+2a_1 x+b_1 ^2 + a_2 ^2x^2+2a_2 x+b_2 ^2 = 1 \\
(1+a_1 ^2+a_2 ^2)x^2 + 2(a_1 b_1 + a_2 b_2 )x + (b_21^2+b_2 ^2-1) = 0 $$

　となり、$a,b,c$を

$$ a = 1+a_1 ^2+a_2 ^2 \\
b = 2(a_1 b_1 + a_2 b_2) \\
c = b_1 ^2 + b_2 ^2 – 1 $$

　とおいて2次方程式の解の公式$x = \frac{-b\pm\sqrt{b^2-4ac}}{2a}$を使って解いてやるとxの値が出ます。直線と球は2点で交わるので、解は2つ求まりますが、撮像面は視点より前を前提とするので、大きい方（ルートの前がプラスの方）の解を採用します。

　ｘが出れば先の直線の式からｙとｚも求まります。

$$ x = \frac{-b + \sqrt{b^2-4ac}}{2a} \\
y = a_1 x + b_1 \\
z = a_2 x + b_2 $$

Pythonで記述

　Pythonで記述してみます。上の式の通りに計算式を並べただけです。使っている記号もそろえてあります。

import numpy as np
import cv2

img_w = 1920
img_h = 1080

senser_w = 0.75
senser_h = 0.75 * img_h / img_w

x1 = -1.2   # 視点の位置
x2 = 0.5 + x1  #　撮像面の位置(必ず視点より前)

w = np.linspace(-senser_w, senser_w, img_w, endpoint=False)
h = np.linspace(-senser_h, senser_h, img_h, endpoint=False)
    
# 配列を対称形にするためのオフセット
w = w + senser_w / img_w
h = h + senser_h / img_h

# センサの座標
ww, hh = np.meshgrid(w, h)

# 直線の式
a1 = ww / (x2 - x1)
a2 = hh / (x2 - x1)
b1 = -a1 * x1
b2 = -a2 * x1

a = 1 + a1**2 + a2**2
b = 2 * (a1 * b1 + a2 * b2)
c = b1**2 + b2**2 - 1

d = (b**2 - 4*a*c) ** (1/2)

# 球面上の3次元座標
x = (-b + d) / (2 * a)
y = a1 * x + b1
z = a2 * x + b2

# 緯度・経度へ変換
phi = np.arcsin(z)
theta = np.arcsin(y / np.cos(phi))

img = cv2.imread("src.jpg")
img_h, img_w = img.shape[:2]

# 画像座標へ正規化（座標を画素位置に戻すため0.5オフセット）
phi = (phi * img_h / np.pi + img_h / 2).astype(np.float32) - 0.5
theta = (theta * img_w / (2 * np.pi) + img_w / 2).astype(np.float32) - 0.5

out = cv2.remap(img, theta, phi, cv2.INTER_CUBIC)
cv2.imwrite("dst.jpg", out)

　簡単に概要を説明します。

　センサ（便宜的にそう呼ぶ）の幅と高さを出力したい解像度（画素数）の間隔でメッシュ(ww,hh)を作ります。対称形にするためのオフセットというのは、-90, -89, -88, … 88, 89, 90 と配列を作ってしまうと、画像サイズが偶数の時に、中心が0にならないため、-89.5 -88.5 … 88.5, 89.5 という形で中心が0で等間隔で並ぶようにオフセットさせています。

w = np.linspace(-senser_w, senser_w, img_w, endpoint=False)
h = np.linspace(-senser_h, senser_h, img_h, endpoint=False)
    
# 配列を対称形にするためのオフセット
w = w + senser_w / img_w
h = h + senser_h / img_h

# センサの座標
ww, hh = np.meshgrid(w, h)

　そのメッシュの各座標と視点を通る直線が球の3次元座標(x,y,z)のどこを通るかを計算しています。先に説明した直線の式から球面の3次元座標を真面目に計算しただけです。

# 球面上の3次元座標
x = (-b + d) / (2 * a)
y = a1 * x + b1
z = a2 * x + b2

　この球の座標の値がそのセンサ位置における画素値になるので、3次元座標を緯度・経度（φ、θ）へ変換して、入力画像の画素値を取得しています。

# 緯度・経度へ変換
phi = np.arcsin(z)
theta = np.arcsin(y / np.cos(phi))

　これを360度写真の座標へ正規化し、remap関数を使って変換しています。座標から画素のindexに戻すために0.5オフセットします。

# 画像座標へ正規化（座標を画素位置に戻すため0.5オフセット）
phi = (phi * img_h / np.pi + img_h / 2).astype(np.float32) - 0.5
theta = (theta * img_w / (2 * np.pi) + img_w / 2).astype(np.float32) -0.5