360度カメラで撮影した写真を変換してやろうと思います。歪みやひずみのないきれいな写真に変換するためにまずはまん丸の画像に変換してみようと思います。ちなみにいわゆるパノラマっぽい任意視点の画像変換に関しては別記事でもう少し本格的に試しています。今回は試しに円へ投影してみます。
正距円筒図法
360度カメラで撮影された画像は、カメラを中心としてぐるっと1周分が1:2の縦横比の画像として記録されています。このフォーマットはいわゆる世界地図と同じように、縦に緯度、横に経度で示した形式になっています。緯度、経度の同じ角度が等間隔になるようにレイアウトされるため、左右に360度、上下に180度、結果として1:2の画像フォーマットになります。

緯度経度は地球の中心から赤道を向いて、ぐるっと一周する向きが経度、見上げる見下げる角度が緯度になります。
equirectangular(エクイレクタングラー)とかそんなフォーマットで呼ばれているようです。有名どころではリコーのシータで撮影するとこんな感じになるようです。この写真は違うけど。
なので地球を同一の経度で輪切りにするといわゆるみかんの実のようになりますし、同一経度で輪切りにすると直径の異なる円が出来上がります。同じ角度でも意味が違います。
出来上がる写真は長方形で見やすく扱いやすいですが、半面上下、いわゆる北極と南極はとてもゆがみます。人の顔とかそこに写ろうものならとても残念な感じになります。
球から円へ投影
今回はこの正距円筒図法で書かれている球を無限遠から真正面で見た円に投影して見ようと思います。正距方位図法に近いですがちょいと違います。
火星から赤道を正面にして見た地球って感じですかね。もしくはある程度距離を離して見た地球儀。
とてもシンプルな変換でわかりやすく、式で表現してもそれほど難しくはないです。
まず赤道で輪切りにします。すると中心からの角度θは経度を意味するので、赤道上からの射影はこの図のようになります。
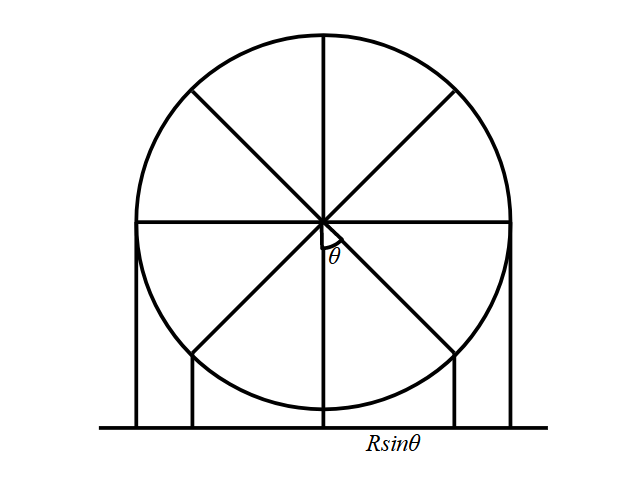
赤道上のとある経度θはx=Rsinθへ射影されます。
では今度は縦に輪切りにします。すると同じように中心からの角度φは緯度を意味することになります。同じように射影するととある緯度φはy=Rsinφへ射影されます。

次に任意の緯度φで輪切りにすることを考えてみます。その断面の円の半径は赤で示すようにR’=Rcosφになります。
今度は任意の緯度φにおける経度θの射影を考えてみます。
前述のように経度φにおける半径R’はRcosφになるので、その時の経度θの射影はx=R’sinθ=Rcosφsinθとなります。
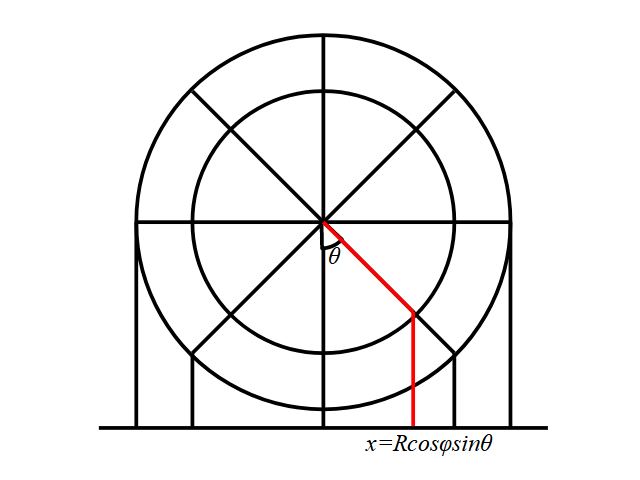
つまり任意の経度θ、緯度φは射影した平面x,yへ
$$ x=R\cos\phi\sin\theta \\
y=R\sin\phi $$
の関係で射影されます。シンプルです。
360度カメラで撮影された全天球画像の縦横はφとθ座標になるので、この全天球画像から真正面から見た平面への写像は
$$ \phi = \arcsin(y/R) \\
\theta = \arcsin(x/R\cos\phi) $$
となります。
Pythonで記述
Pythonで記述してみます。
import cv2
import numpy as np
img = cv2.imread("src.jpg")
h,w = img.shape[:2]
w = w//2
h = h//2
r = h
X, Y = np.meshgrid(np.arange(-w,w), np.arange(-h,h))
phi = np.arcsin(Y/r)
theta = np.arcsin(X / (r * np.cos(phi)))
Y = (2 * phi / np.pi) * h + h #正規化+オフセット
X = (2 * theta / np.pi) * w + w
out = cv2.remap(img, X.astype(np.float32), Y.astype(np.float32), cv2.INTER_CUBIC)
cv2.imwrite("dst.jpg",out)
かなりシンプルです。OpenCVのremapという関数のおかげでたいそう簡単な記述で済んでしまいました。phiとthetaの値が-π/2 から π/2の間の値になるので、画像の幅と高さで正規化しつつ、中心座標を左上にずらすためにオフセットをさせています。
ただしこのまま実行すると、
RuntimeWarning: invalid value encountered in arcsin
theta = np.arcsin(X / (r * np.cos(phi)))
こんなワーニングが出ます。arcsinの引数が1を超えるのだと思います。ただこれでも計算結果にnanが入るだけで、それっぽい結果が出てしまいます。まぁ無視しときます。
こんな入力画像を入れると、

こんな結果になります。まぁ想定通りです。

試しにとった写真をソースにすると

こんな感じ。

魚眼レンズで撮影したかのような写真になります。
まとめ
本当は全天球画像のビューアーを作ろうと思っていろいろいじり始めたのですが、目的のものとは少し違うものができちゃいました。そうかこんなモデルではないんだな。ということがわかったのでよしとします。
次はちゃんとしたビューアーを作ってやろうと思います。


コメント