360度カメラで撮影した写真を任意の視点からの画像(パノラマ画像)へ変換するビューアーを作ってみようと思います。3回シリーズの今回はその2回目です。
1.360度写真の平面投影
2.視点の変更と背面の投影
3.視点の回転
前回の記事でひとまず適当な全天球画像(エクイレクタングラー画像)からそれっぽい画像(切り出したパノラマ画像)へ変換することはできました。
今回はその続きです。最適な視点の考察と、描画範囲を広げて裏側もきちんと描画したいと思います。
視点の最適化
前回の記事で開設したように、全天球画像に対して視点の位置関係のイメージは

こんな感じ。とりあえず青で示した位置で見えるであろうパノラマ画像を作ることを目指して計算したので、平面への描画パラメータが適当でした。かなりゆがんで見えます。
入力の画像がこれだと

取得される画像は

中心は細長く、すみっこは太ってます。これはこれでありなのですが、お手本としているTHETAのビューアーだと
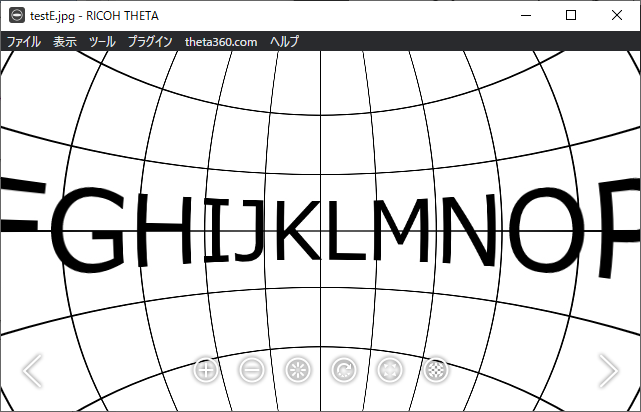
だいぶ様子が違います。重ねるとこんな感じになります。

赤いのがお手本とするビューアー。写っている範囲は似ていますが、だいぶ歪んでいます。OやGの横方向の伸び方とか見るとだいぶ違いますね。この違いを何とかします。
前回のコードにて視点と撮像面の位置関係は、
視点位置の座標 x1 = -0.5
撮像面 x2 = 0
センサ幅 1.5
で変換したものです。図にすると
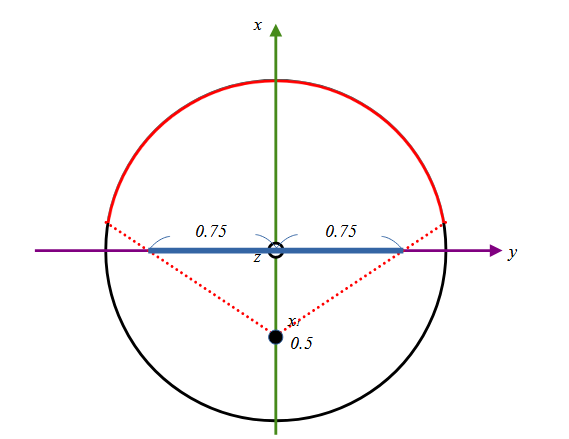
視点と撮像面が近すぎてかなり視野角がかなり広角になっていることがわかります。まったく補正のない広角レンズで近くの写真をとった時のそれと同じことですね。そこで少し望遠気味に視点をずらしてみます。

視点を遠ざけたうえで、同じサイズの撮像面にへ投影すると、だいぶ角度が狭くなります。赤で示す写りこむ範囲は同じなのですが、取得される画像の歪みは改善されます。その時のパラメータは
視点位置の座標 x1 = -1.0
撮像面 x2 = -0.17
センサ幅 1.5

こんな感じ。見本としているビューアーとほぼ同じような画像が取得できました。実画像で試しても以前の視点だと

これが

こうなります。先の画像よりバイクの縦横のバランスが良い気がします。
試しにもう少し引いてみます。
視点位置の座標 x1 = -2.0
撮像面 x2 = -0.43
センサ幅 1.5
位置関係はこれ。
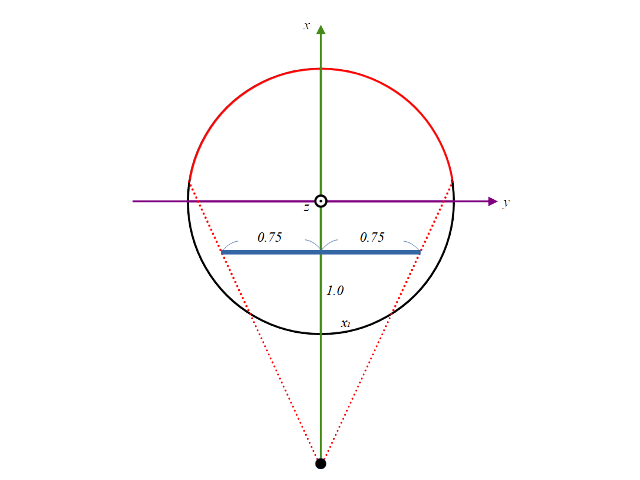
だいぶ視覚は狭くなりますが撮像面までの距離を調整して同じような範囲が写るように調整します。すると得られる画像は

こんな感じ。また少しまっすぐになってきます。このようにパラメータを調整することで得られる画像の様子を変えることができます。
裏側
調子に乗ってパラメータをいじってみると…。

あれ?裏側がおかしいことに気づきます。ABCDEとQRSTUが写って来ていないです。鏡の如く文字が折り返っています。
視点の関係としてはこんな感じです。
視点の座標 x1 = -1.2
撮像面の座標 x2 = -0.7
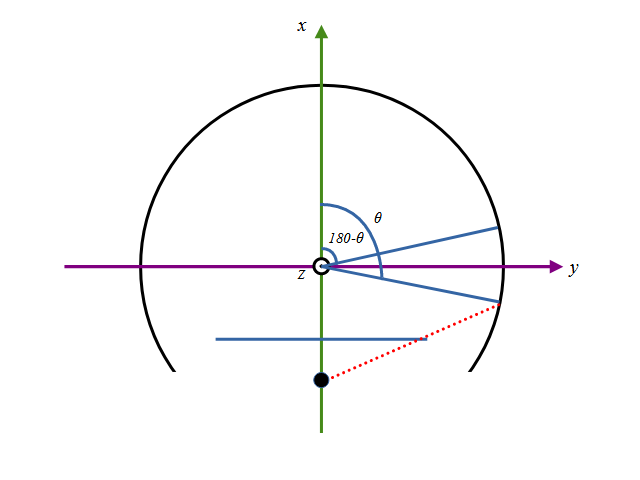
本来写りこんできてほしい経度θが180-θに化けています。
これはこの座標(経度)θを求める際にarcsinを使っているのでどうしても発生してしまいます。θの式を思い出すと
$$ \phi = \arcsin (z) \\
\theta = \arcsin ( \frac{y}{\cos \phi}) $$
arcsinの値は-90度~90度なので、その値を外れる角度は求めることができません。緯度にあたるφは-90~90なので問題ありませんが、経度にあたるθはそうもいきません。-180~-90度と90~180度は元のx,yの値から何とかして補正します。
これにはθに変換する元の座標x,yの符号を考慮することで補正することができます。
まずはxの符号。xの符号が正の時は得られたarcsinで得られたθの値はそのまま信じられますが、負の場合は裏側になるので、下の図のようにπ-θか-π-θへ変換する必要があります。
次にこの補正値πまたは-πの切り替えはyの符号を見るとわかります。yの符号が正の時はπ、負の時は-πすることでθの変換が可能になります。
図のように
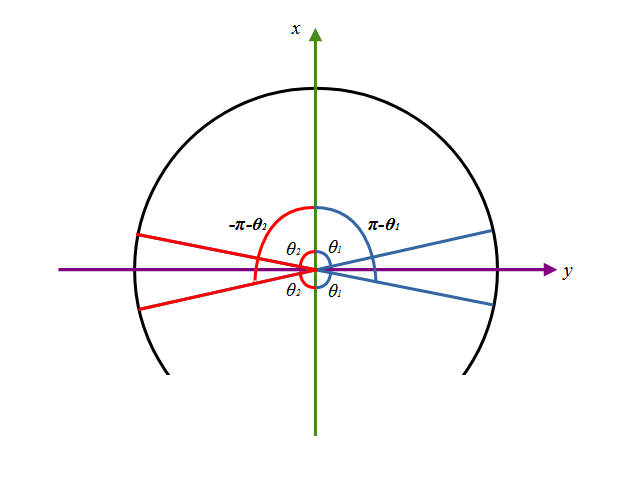
x<0かつy>0であればθ=π-θ
x<0かつy<0であればθ=-π-θ
となります。
象限ごとにまとめると、
x > 0 かつ y > 0 では θ=θ
x > 0 かつ y < 0 では θ=θ
x < 0 かつ y > 0 では θ = π-θ
x < 0 かつ y < 0 では θ = -π-θ
となります。
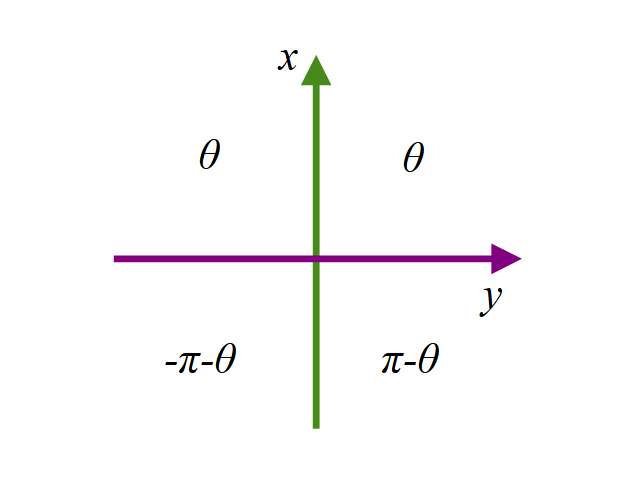
このルールにしたがって得られたθを補正すると裏側も正しく写りこませることができます。
Pythonで記述
関数に分けましたが、ほぼ前回の記述のままです。裏側の映り込みを考慮した記述を追加しただけです。
import numpy as np
import cv2
##
# @brief 3次元座標群切り出し関数
# @details とある視点からとある距離の平面を通る半径1の球の表面を結んだ交点座標群を切り出す
# @param img_w 画像の幅(分解能)
# @param img_h 画像の高さ(分解能)
# @param senser_size センサに見立てた平面の大きさ(0以上の少数)
# @param view_point 視点位置
# @param senser_point 視点から平面までの距離
# @return x,y,zの座標群
def create_3dmap_from_viewpoint(img_w, img_h, senser_size, view_point, senser_point):
senser_w = senser_size
senser_h = senser_size * img_h / img_w
x1 = view_point # 視点の位置
x2 = view_point + senser_point # 撮像面の位置(必ず視点より前)
w = np.linspace(-senser_w, senser_w, img_w, endpoint=False)
h = np.linspace(-senser_h, senser_h, img_h, endpoint=False)
# 配列を対称形にするためのオフセット
w = w + senser_w / img_w
h = h + senser_h / img_h
# センサの座標
ww, hh = np.meshgrid(w, h)
# 直線の式
a1 = ww / (x2 - x1)
a2 = hh / (x2 - x1)
b1 = -a1 * x1
b2 = -a2 * x1
a = 1 + a1**2 + a2**2
b = 2 * (a1 * b1 + a2 * b2)
c = b1**2 + b2**2 - 1
d = (b**2 - 4*a*c) ** (1/2)
# 球面上の3次元座標
x = (-b + d) / (2 * a)
y = a1 * x + b1
z = a2 * x + b2
return x, y, z
##
# @brief 緯度経度群を取得する関数
# @details 半径1の球上の3次元座標群を緯度経度表記に変換する
# @param x x座標群
# @param y y座標群
# @param z z座標群
# @return 緯度、経度群(ラジアン)
def conv_equirectangularmap(x, y, z):
# 緯度・経度へ変換
phi = np.arcsin(z)
theta = np.arcsin(np.clip(y / np.cos(phi), -1, 1))
theta = np.where((x<0) & (y<0), -np.pi-theta, theta)
theta = np.where((x<0) & (y>0), np.pi-theta, theta)
return phi, theta
##
# @brief 緯度経度情報にしたがって画像を変換する関数
# @details 1:2で格納されている画像から、そのx,y座標を緯度経度と見立てて対応する座標変換を行う
# @param img 元となる360度画像(1:2)
# @param phi 緯度(縦方向 ラジアン)
# @param theta 経度(横方向 ラジアン)
# @return 変換された画像
def remap_equirectangular(img, phi, theta, interpolation=cv2.INTER_CUBIC, borderMode=cv2.BORDER_WRAP):
img_h, img_w = img.shape[:2]
# 画像座標へ正規化(座標を画素位置に戻すため0.5オフセット)
phi = (phi * img_h / np.pi + img_h / 2).astype(np.float32) - 0.5
theta = (theta * img_w / (2 * np.pi) + img_w / 2).astype(np.float32) - 0.5
return cv2.remap(img, theta, phi, interpolation, borderMode = borderMode)
img = cv2.imread("src.jpg")
x, y, z = create_3dmap_from_viewpoint(1920, 1080, 0.75, -1.2, 0.5)
phi, theta = conv_equirectangularmap(x,y,z)
out = remap_equirectangular(img, phi, theta)
cv2.imwrite("dst.jpg", out)
差分は象限ごとに補正値を計算している
theta = np.where((x<0) & (y<0), -np.pi-theta, theta)
theta = np.where((x<0) & (y>0), np.pi-theta, theta)
この部分だけです。
またremapに与えるborderModeですが、座標を求める元画像が循環しているので、cv2.BORDER_WRAPを使うのがベストと判断しました。初めて使いどころがわかりました。
結果
先ほどと同じようにこれを入力として使います。

すると思惑通り、裏側が正しく映りこみました。

正しく裏側にあたるCDEとQRSが映り込みました。
まとめと今後
だいぶビューアーとしていい感じに出来上がってきました。パラメータを調整することで意図通りの画像が得られそうですし、また裏側もちゃんと描画できるようになりました。



コメント