 python
python 画像認識の有名なCNN
像認識を行うことを目的とした代表的なCNNのメモ。これをキーワードにググる。ほうぼう調べた内容のメモなので内容は薄い。
ちなみに有名なモデルは学習済みのデータも含めて公開されているので気軽に試すことができる。
AlexNet
...
 python
python  python
python  python
python 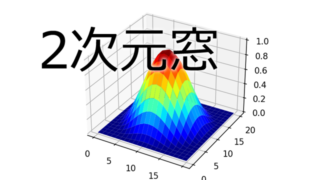 python
python 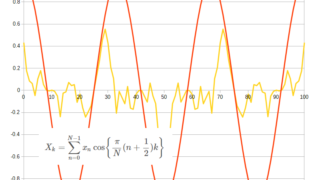 メモ
メモ 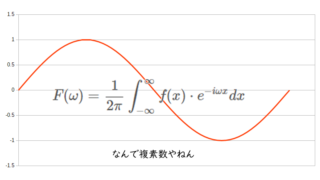 python
python 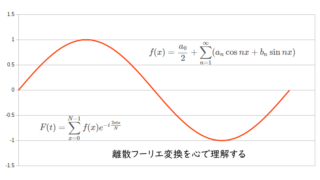 メモ
メモ  python
python  python
python  python
python